【题目】欧城物业为美化小区,要对面积为9600平方米的区域进行绿化,计划安排甲、乙两个园林队完成,已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍,并且甲、乙两园林队独立完成面积为800平方米区域的绿化时,甲园林队比乙园林队少用2天.
(1)求甲、乙两园林队每天能完成绿化的面积分别是多少平方米.
(2)物业每天需付给甲园林队的绿化费用为0.4万元,乙园林队的绿化费用为0.25万元,如果这次绿化总费用不超过10万元,那么欧城物业至少应安排甲园林队工作多少天?
参考答案:
【答案】(1)甲、乙两园林队每天能完成绿化的面积分别是400平方米和200平方米;(2)甲工程队至少应工作20天.
【解析】
(1)设乙园林队每天能完成的绿化面积为x平方米,则甲园林队每天能完成的绿化面积为2x平方米,根据工作时间=工作总量÷工作效率,结合甲队比乙队少用2天,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)设应安排甲园林队工作y天,则乙园林队工作![]() =(48﹣2y)天,根据总费用=0.4×甲园林队工作天数+0.25×乙园林队工作天数,结合总费用不超过10万元,即可得出关于y的一元一次不等式,解之即可得出y的取值范围,取其内的最小值即可.
=(48﹣2y)天,根据总费用=0.4×甲园林队工作天数+0.25×乙园林队工作天数,结合总费用不超过10万元,即可得出关于y的一元一次不等式,解之即可得出y的取值范围,取其内的最小值即可.
(1)设乙园林队每天能完成绿化的面积为x平方米,则甲园林队每天能完成绿化的面积为2x平方米,
根据题意得:![]() ,
,
解得:x=200,
经检验,x=200是原分式方程的解,
∴当x=200时,2x=400;
答:甲、乙两园林队每天能完成绿化的面积分别是400平方米和200平方米;
(2)设欧城物业应安排甲园林队工作y天,则乙园林队工作![]() =(48﹣2y)天,
=(48﹣2y)天,
根据题意得:0.4y+0.25(48﹣2y)≤10,
解得:y≥20,
∴y的最小值为20.
答:甲工程队至少应工作20天.
故答案为:(1)甲、乙两园林队每天能完成绿化的面积分别是400平方米和200平方米;(2)甲工程队至少应工作20天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=m时,多项式x2+2x+n2的值为﹣1,则x=﹣m时,该多项式的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产
 、
、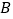 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件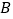 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.(1)设生产
 种产品
种产品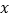 件,完成表格:
件,完成表格: 产品
产品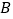 产品
产品生产数量(件
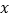 件
件件
需甲种原料(千克)
需乙种原料(千克)
(2)按要求安排
 、
、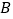 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.(3)以上方案哪种利润最大?是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=
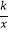 (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 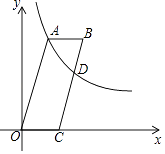
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|﹣4|﹣(﹣2)2+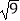 ﹣(
﹣(  )0
)0
(2)解不等式组 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
相关试题

