搜索
【题目】如何求tan75°的值？按下列方法作图可解决问题.如图，在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，延长CB至点M，在射线BM上截取线段BD，使BD=AB，连接AD.连接此图可求得tan75°的值为（ ）
A.2- 
B.2+
C.1+
D.
-1
参考答案：
【答案】B
【解析】解：在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，
则AB=2AC=2k，BC= 
AC= k.
∵BD=AB=2k，
∴CD=BC+BD=（ +2）k，∠BDA= 
∠ABC=15°，
∴∠CAD=75°，
则在Rt△ACD中，tan75°=tan∠CAD= 
.
故选B.
解直角三角形，求正切值时，需要知道直角三角形的两条边，由AC=k，则易得CD的长，而∠CAD=75°，即可解答.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形OABC是平行四边形，点C在x轴上，反比例函数y=
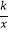（x＞0）的图象经过点A（5，12），且与边BC交于点D．若AB=BD，则点D的坐标为 ．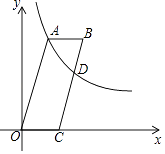 
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
（1）计算：|﹣4|﹣（﹣2）2+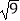
﹣（ 
）0
（2）解不等式组
． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（ ）
A. ∠1＝∠3 B. ∠B＋∠BCD＝180°
C. ∠2＝∠4 D. ∠D＋∠BAD＝180°
-
科目： 来源： 题型：
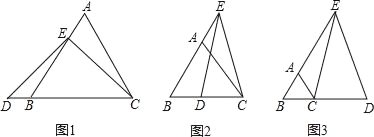
查看答案和解析>>【题目】已知△ABC为等边三角形，E为射线BA上一点，D为直线BC上一点，ED＝EC．
（1）当点E在AB的上，点D在CB的延长线上时（如图1），求证：AE+AC＝CD；
（2）当点E在BA的延长线上，点D在BC上时（如图2），猜想AE、AC和CD的数量关系，并证明你的猜想；
（3）当点E在BA的延长线上，点D在BC的延长线上时（如图3），请直接写出AE、AC和CD的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知下列方程：①
；②0.3x＝1；③
；④x2﹣4x＝3；⑤x＝6；⑥x+2y＝0．其中一元一次方程的个数是（ ）A. 2B. 3C. 4D. 5
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况，随机抽取了50名学生，并统计他们平均每天的课外阅读时间t（单位：min），然后利用所得数据绘制成如图不完整的统计图表．
课外阅读时间频数分布表课外阅读时间t
频数
百分比
10≤t＜30
4
8%
30≤t＜50
8
16%
50≤t＜70
a
40%
70≤t＜90
16
b
90≤t＜110
2
4%
合计
50
100%
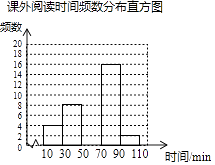
请根据图表中提供的信息回答下列问题：
（1）a= ， b=；
（2）将频数分布直方图补充完整；
（3）若全校有900名学生，估计该校有多少学生平均每天的课外阅读时间不少于50min？
相关试题
