【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产![]() 、
、![]() 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件![]() 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件![]() 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
(1)设生产![]() 种产品
种产品![]() 件,完成表格:
件,完成表格:
|
| |
生产数量(件 |
| 件 |
需甲种原料(千克) |
|
|
需乙种原料(千克) |
|
|
(2)按要求安排![]() 、
、![]() 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.
(3)以上方案哪种利润最大?是多少元?
参考答案:
【答案】(1)见解析;(2)见解析;(3) 采用方案①所获利润最大,为45000元.
【解析】
(1)根据“A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克,乙种原料3千克;生产一件B种产品需用甲种原料4千克,乙种原料10千克”可得答案;
(2)首先找出题中的等量关系即甲种原料不超过360千克,乙种原料不超过290千克,然后列出不等式组并求出它的解集.由此可确定出具体方案.
(3)本题可将三种方案的最大利润都求出来,再进行比较即可.
(1)补全表格如下:
A产品 | B产品 | |
生产数量(件) | x件 | (50-x)件 |
需甲种原料(千克) | 9x | 4(50-x) |
需乙种原料(千克) | 3x | 10(50-x) |
(2)根据题意有:![]() ,
,
解得:30≤x≤32,
所以有三种方案:①安排A种产品30件,B种产品20件;
②安排A种产品31件,B种产品19件;
③安排A种产品32件,B种产品18件.
(2)(2)∵方案一为:700×30+1200×20=45000元;
方案二为:700×31+1200×19=44500元;
方案三为:700×32+1200×18=44000元.
采用方案①所获利润最大,为45000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方2
 米处的点C出发,沿斜面坡度i=1:
米处的点C出发,沿斜面坡度i=1:  的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈  ,cos37°≈
,cos37°≈  ,tan37°≈
,tan37°≈  .计算结果保留根号)
.计算结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=m时,多项式x2+2x+n2的值为﹣1,则x=﹣m时,该多项式的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】欧城物业为美化小区,要对面积为9600平方米的区域进行绿化,计划安排甲、乙两个园林队完成,已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍,并且甲、乙两园林队独立完成面积为800平方米区域的绿化时,甲园林队比乙园林队少用2天.
(1)求甲、乙两园林队每天能完成绿化的面积分别是多少平方米.
(2)物业每天需付给甲园林队的绿化费用为0.4万元,乙园林队的绿化费用为0.25万元,如果这次绿化总费用不超过10万元,那么欧城物业至少应安排甲园林队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=
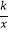 (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 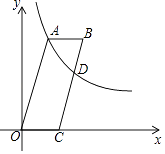
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|﹣4|﹣(﹣2)2+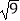 ﹣(
﹣(  )0
)0
(2)解不等式组 .
.
相关试题

