【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y= ![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 .
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为 . 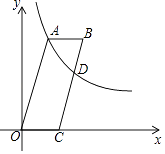
参考答案:
【答案】(8,![]() )
)
【解析】解:∵反比例函数y= ![]() (x>0)的图象经过点A(5,12),
(x>0)的图象经过点A(5,12),
∴k=12×5=60,
∴反比例函数的解析式为y= ![]() ,
,
设D(m, ![]() ),
),
由题可得OA的解析式为y= ![]() x,AO∥BC,
x,AO∥BC,
∴可设BC的解析式为y= ![]() x+b,
x+b,
把D(m, ![]() )代入,可得
)代入,可得 ![]() m+b=
m+b= ![]() ,
,
∴b= ![]() ﹣
﹣ ![]() m,
m,
∴BC的解析式为y= ![]() x+
x+ ![]() ﹣
﹣ ![]() m,
m,
令y=0,则x=m﹣ ![]() ,即OC=m﹣
,即OC=m﹣ ![]() ,
,
∴平行四边形ABCO中,AB=m﹣ ![]() ,
,
如图所示,过D作DE⊥AB于E,过A作AF⊥OC于F,则△DEB∽△AFO,
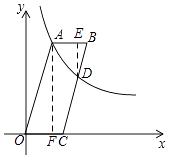
∴ ![]() =
= ![]() ,而AF=12,DE=12﹣
,而AF=12,DE=12﹣ ![]() ,OA=
,OA= ![]() =13,
=13,
∴DB=13﹣ ![]() ,
,
∵AB=DB,
∴m﹣ ![]() =13﹣
=13﹣ ![]() ,
,
解得m1=5,m2=8,
又∵D在A的右侧,即m>5,
∴m=8,
∴D的坐标为(8, ![]() ).
).
所以答案是:(8, ![]() ).
).
【考点精析】通过灵活运用平行四边形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产
 、
、 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.(1)设生产
 种产品
种产品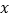 件,完成表格:
件,完成表格: 产品
产品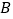 产品
产品生产数量(件
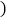
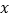 件
件件
需甲种原料(千克)
需乙种原料(千克)
(2)按要求安排
 、
、 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.(3)以上方案哪种利润最大?是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】欧城物业为美化小区,要对面积为9600平方米的区域进行绿化,计划安排甲、乙两个园林队完成,已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍,并且甲、乙两园林队独立完成面积为800平方米区域的绿化时,甲园林队比乙园林队少用2天.
(1)求甲、乙两园林队每天能完成绿化的面积分别是多少平方米.
(2)物业每天需付给甲园林队的绿化费用为0.4万元,乙园林队的绿化费用为0.25万元,如果这次绿化总费用不超过10万元,那么欧城物业至少应安排甲园林队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|﹣4|﹣(﹣2)2+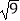 ﹣(
﹣(  )0
)0
(2)解不等式组 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如何求tan75°的值?按下列方法作图可解决问题.如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD.连接此图可求得tan75°的值为( )

A.2-
B.2+
C.1+
D.
-1
相关试题

