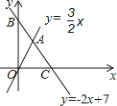
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线![]() 相交于点A.
相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线![]() 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)A点坐标是(2,3);(2)P点坐标是(0,![]() );(3)存在;点Q是坐标是((
);(3)存在;点Q是坐标是((![]() ,
,![]() ))或(
))或(![]() ,
,![]() )).
)).
【解析】(1)联立方程,解方程即可求得;
(2)设P点坐标是(0,y),根据勾股定理列出方程,解方程即可求得;
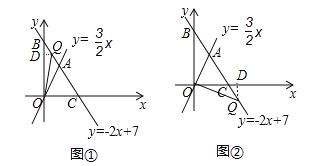
(3)分两种情况:①当Q点在线段AB上:作QD⊥y轴于点D,则QD=x,根据S△OBQ=S△OAB﹣S△OAQ列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=﹣y,根据S△OCQ=S△OAQ﹣S△OAC列出关于y的方程解方程求得即可.
(1)解方程组: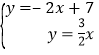 得:
得:![]() ,
,
∴A点坐标是(2,3);
(2)设P点坐标是(0,y).
∵△OAP是以OA为底边的等腰三角形,∴OP=PA,∴22+(3﹣y)2=y2,解得:y=![]() ,∴P点坐标是(0,
,∴P点坐标是(0,![]() ).
).
故答案为:(0,![]() );
);
(3)存在;
由直线y=﹣2x+7可知B(0,7),C(![]() ,0).
,0).
∵S△AOC=![]() ×
×![]() ×3=
×3=![]() <6,S△AOB=
<6,S△AOB=![]() ×7×2=7>6,∴Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y).
×7×2=7>6,∴Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y).
当Q点在线段AB上:作QD⊥y轴于点D,如图①,则QD![]() OBQD=1,即
OBQD=1,即![]() ×7x=1,∴x=
×7x=1,∴x=![]() ,把x=
,把x=![]() 代入y=﹣2x+7,得y=
代入y=﹣2x+7,得y=![]() ,∴Q的坐标是(
,∴Q的坐标是(![]() );
);
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图②则QD=﹣y,∴S△OCQ=S△OAQ﹣S△OAC=6﹣![]() =
=![]() OCQD=
OCQD=![]() ,即
,即![]() ×
×![]() ×(﹣y)=
×(﹣y)=![]() ,∴y=﹣
,∴y=﹣![]() ,把y=﹣
,把y=﹣![]() 代入y=﹣2x+7,解得x=
代入y=﹣2x+7,解得x=![]() ,∴Q的坐标是(
,∴Q的坐标是(![]() ,﹣
,﹣![]() ).
).
综上所述:点Q是坐标是(![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)当a≠0时,求
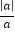 的值.(写出解答过程)
的值.(写出解答过程)(2)若a≠0,b≠0,且
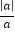 +
+ =0,则
=0,则 的值为 .
的值为 .(3)若ab>0,则
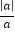 +
+ +
+ 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在反比例函数
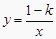 的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.-1
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④
 小时后两人相遇.
小时后两人相遇.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线
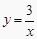 (x>0)上的一个动点,PB⊥y轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会( ) 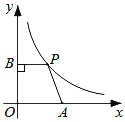
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点A(-1,
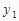 )、B(1,
)、B(1, 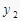 )、C(2,
)、C(2, 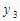 )是反比例函数
)是反比例函数 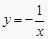 图象上的三个点,则下列结论正确的是( )
图象上的三个点,则下列结论正确的是( )
A.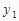 >
> 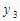 >
> 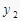
B.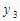 >
> 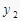 >
> 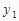
C.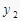 >
> 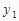 >
> 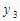
D.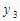 >
> 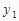 >
> 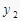
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点 E、F 分别在边 BC、CD 上,且 BE=CF.连接 AE、BF.下列结论错误的是()

A. AE=BF B. AE⊥BF C. ∠DAE=∠BFC D. ∠AEB+∠BFC=1200
相关试题

