【题目】如图,正方形ABCD中,点 E、F 分别在边 BC、CD 上,且 BE=CF.连接 AE、BF.下列结论错误的是()

A. AE=BF B. AE⊥BF C. ∠DAE=∠BFC D. ∠AEB+∠BFC=1200
参考答案:
【答案】D
【解析】根据正方形的性质可以证明△ABE≌△BCF,可以得出AE=BF,∠BAE=∠CBF,再由直角三角形的性质就可以得出∠BGE=90°,由∠BAE+∠AEB=90°,∠CBF+∠AEB=90°可得∠DAE=∠BFC,无法说明∠AEB+∠BFC=120°.
A.∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠BCD=90°.
在△ABE与△BCF中
AB=BC,∠ABE=∠BCF,BE=CF
∴△ABE≌△BCF(SAS)
∴AE=BF;
故A正确;
(2)由△ABE≌△BCF
∴∠BAE=∠CBF.
∵∠ABE=90°
∴∠BAE+∠AEB=90°
∴∠CBF+∠AEB=90°
∴∠BGE=90°
∴AE⊥BF.
故B正确;
C. ∵∠BAE=∠CBF,
∠BAE+∠AEB=90°,∠CBF+∠AEB=90°,
∴∠DAE=∠BFC,
故C正确;
D.无法说明∠AEB+∠BFC=120°,故D不正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
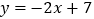 与
与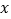 轴、
轴、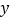 轴分别相交于点C、B,与直线
轴分别相交于点C、B,与直线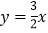 相交于点A.
相交于点A.(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(3)在直线
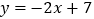 上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.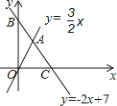
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线
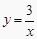 (x>0)上的一个动点,PB⊥y轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
(x>0)上的一个动点,PB⊥y轴于点B , 当点P的横坐标逐渐增大时,四边形OAPB的面积将会( ) 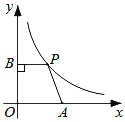
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点A(-1,
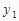 )、B(1,
)、B(1, 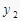 )、C(2,
)、C(2, 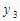 )是反比例函数
)是反比例函数 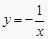 图象上的三个点,则下列结论正确的是( )
图象上的三个点,则下列结论正确的是( )
A.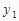 >
> 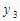 >
> 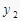
B.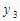 >
> 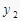 >
> 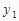
C.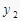 >
> 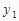 >
> 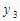
D.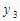 >
> 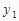 >
> 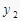
-
科目: 来源: 题型:
查看答案和解析>>【题目】若反比例函数
 的图象经过点(m , 3m),其中m≠0,则此反比例函数图象经过( )
的图象经过点(m , 3m),其中m≠0,则此反比例函数图象经过( )
A.第一、三象限
B.第一、二象限
C.第二、四象限
D.第三、四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知CD=6m,AD=8m,∠ADC=90°,BC=24m,AB=26m.图中阴影部分的面积=_____m2.

-
科目: 来源: 题型:
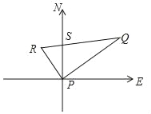
查看答案和解析>>【题目】如图,某港口P位于东西方向的海岸线上,A、B两艘轮船同时从港口P出发,各自沿一固定方向航行,A轮船每小时航行12海里,B轮船每小时航行16海里.它们离开港口一个半小时后分别位于点R、Q处,且相距30海里.已知B轮船沿北偏东60°方向航行.
(1)A轮船沿哪个方向航行?请说明理由;
(2)请求出此时A轮船到海岸线的距离.
相关试题

