搜索
【题目】在反比例函数 
的图象的每一条曲线上，y都随x的增大而增大，则k的值可以是（ ）
A.-1
B.0
C.1
D.2
参考答案：
【答案】D
【解析】解答：反比例函数 
的图象上的每一条曲线上，y随x的增大而增大， ∴1-k＜0，
∴k＞1．
故选：D．
分析：对于函数 
来说，当k＜0时，每一条曲线上，y随x的增大而增大；当k＞0时，每一条曲线上，y随x的增大而减小．易错点：对解析式 中k的意义不理解，直接认为k＜0，错选A．
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识，掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．
-
科目： 来源： 题型：
查看答案和解析>>【题目】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合，研究数轴我们发现：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB＝|a﹣b|，线段AB的中点表示的数为
．如：如图，数轴上点A表示的数为﹣2，点B表示的数为8，则A、两点间的距离AB＝|﹣2﹣8|＝10，线段AB的中点C表示的数为
＝3，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动．设运动时间为t秒（t＞0）．（1）用含t的代数式表示：t秒后，点P表示的数为 ，点Q表示的数为 ．
（2）求当t为何值时，P、Q两点相遇，并写出相遇点所表示的数；
（3）求当t为何值时，PQ＝
AB；（4）若点M为PA的中点，点N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两车分别从A地将一批物品运往B地，再返回A地，图6表示两车离A地的距离s（千米）随时间t（小时）变化的图象，已知乙车到达B地后以30千米/小时的速度返回．请根据图象中的数据回答：
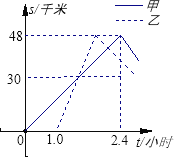
（1）甲车出发多长时间后被乙车追上？
（2）甲车与乙车在距离A地多远处迎面相遇？
（3）甲车从B地返回的速度多大时，才能比乙车先回到A地？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）当a≠0时，求
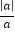的值．（写出解答过程）（2）若a≠0，b≠0，且
+
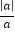=0，则
的值为 ．（3）若ab＞0，则
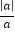++的值为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】A，B两地相距80km，甲、乙两人骑车分别从A，B两地同时相向而行，他们都保持匀速行驶．如图，l1，l2分别表示甲、乙两人离B地的距离y（km）与骑车时间x（h）的函数关系．根据图象得出的下列结论，正确的个数是（ ）
①甲骑车速度为30km/小时，乙的速度为20km/小时；
②l1的函数表达式为y=80﹣30x；
③l2的函数表达式为y=20x；
④
小时后两人相遇．
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
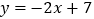与
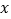轴、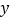
轴分别相交于点C、B，与直线
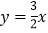相交于点A．（1）求A点坐标；
（2）如果在y轴上存在一点P，使△OAP是以OA为底边的等腰三角形，求P点坐标；
（3）在直线
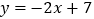上是否存在点Q，使△OAQ的面积等于6？若存在，请求出Q点的坐标，若不存在，请说明理由．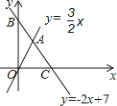
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A是x轴正半轴上的一个定点，点P是双曲线
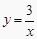（x＞0）上的一个动点，PB⊥y轴于点B ， 当点P的横坐标逐渐增大时，四边形OAPB的面积将会（ ）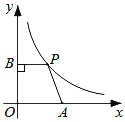 
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
相关试题
