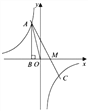
【题目】如图,已知反比例函数![]() 的图象经过第二象限内的点A(
的图象经过第二象限内的点A(![]() ,4),AB⊥x轴于点B,△AOB的面积为2,若直线
,4),AB⊥x轴于点B,△AOB的面积为2,若直线![]() 经过点A,并且经过反比例函数
经过点A,并且经过反比例函数![]() 的图象上另一点C(2,
的图象上另一点C(2,![]() ).
).
(1)求反比例函数和直线的解析式;
(2)设直线![]() 与
与![]() 轴交于点M,求AM的长.
轴交于点M,求AM的长.
参考答案:
【答案】(1) ![]() ,y=﹣2x+2;(2)2
,y=﹣2x+2;(2)2![]()
【解析】分析:
(1)由题意易得S△AOB=![]() AB·
AB·![]() ,这样结合已知条件即可求得m的值,从而可得点A的坐标,由点A的坐标求得k的值,即可得到反比例函数的解析式,再将点C的坐标代入所得的解析式求得n的值,可得点C的坐标,这样由直线
,这样结合已知条件即可求得m的值,从而可得点A的坐标,由点A的坐标求得k的值,即可得到反比例函数的解析式,再将点C的坐标代入所得的解析式求得n的值,可得点C的坐标,这样由直线![]() 过点A、C即可求得一次函数的解析式了;
过点A、C即可求得一次函数的解析式了;
(2)由(1)中所得一次函数的解析式求得点M的坐标,由此可得BM的长,这样结合AB的长即可由勾股定理求得AM的长了.
(1)∵点A(m,4)在第二象限,即AB=4,OB=|m|,
∵S△AOB=![]() AB·OB=
AB·OB=![]() AB·
AB·![]() ,
,
解得: |m|=1,
∴A (-1,4)
∵点A(-1,4)在反比例函数![]() 的图像上
的图像上
∴k=-4,
∴反比例函数解析式为![]() ,
,
又∵反比例函数![]() 的图象经过C(2,n)
的图象经过C(2,n)
∴n=-2,
∴C (2,﹣2),
∵直线y=ax+b过点A (﹣1,4),C (2,﹣2)
∴ ![]() ,
,
解方程组得:![]() ,
,
∴直线y=ax+b的解析式为y=﹣2x+2;
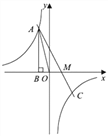
(2)当y=0时,即﹣2x+2=0,
解得x=1,
∴点M的坐标是M(1,0),
在Rt△ABM中,∵AB=4,BM=BO+OM=1+1=2,
∴AM=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P,Q分别从A,B两点同时出发,在数轴上运动,它们的速度分别是2个单位长度/s、4个单位长度/s,它们运动的时间为t s.
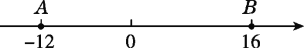
(1)如果点P,Q在点A,B之间相向运动,当它们相遇时,点P对应的数是________;
(2)如果点P,Q都向左运动,当点Q追上点P时,求点P对应的数;
(3)如果点P,Q在点A,B之间相向运动,当PQ=8时,求点P对应的数.
-
科目: 来源: 题型:
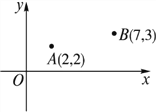
查看答案和解析>>【题目】A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7, 3),根据下列要求作图(保留作图痕迹,不用写作法).
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A,B两校的距离相等?如果有,请用尺规作图找出该点;
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,P点的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
①-3,9,-27,81,-243,729,…;
②0,12,-24,84,-240,732,…;
③-1,3,-9,27,-81,243,….
(1)第①行数有什么规律?
(2)第②行数与第①行数有什么关系?
(3)第③行数与第①行数有什么关系?
(4)取每行数的第10个数,计算这三个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C三点在同一条直线上,若AB=10cm,BC=4cm,D是线段AC的中点,则AD的长为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

相关试题

