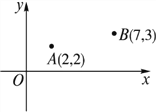
【题目】A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7, 3),根据下列要求作图(保留作图痕迹,不用写作法).
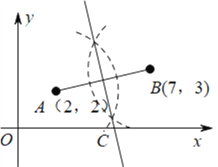
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A,B两校的距离相等?如果有,请用尺规作图找出该点;
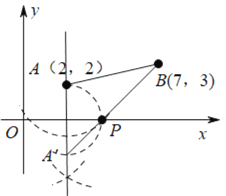
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,P点的坐标为________.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】分析:
(1)由到平面内两点距离相等的点在连接这两点所得线段的垂直平分线上可知,连接AB,作AB的垂直平分线,所作直线与x轴的交点即为所求点C;
(2)作出点A关于x轴的对称点A′,连接A′B与x轴的交点即为所求的点P;
详解:
(1)如下图,图中点C为所求点;
(2)如下图所示,图中点P为所求的点;
∵点A′和点A(2,2)关于x轴对称,
∴点A′的坐标为(2,-2),
设直线A′B的解析式为:![]() ,代入点A′和点B的坐标可得:
,代入点A′和点B的坐标可得:
![]() ,解得:
,解得:![]() ,
,
∴直线A′B的解析式为:![]() ,
,
∵在![]() 中,当
中,当![]() 时,可得
时,可得![]() ,
,
∴点P的坐标为(4,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用方程解答下列问题
(1)一件工作,甲单独做20小时完成,乙单独做12小时完成,现在先由甲单独做4小时,余下的由甲乙一起完成余下的部分需要几小时完成?
(2)王强参加了一场3000米的赛跑,他以6米/秒的速度跑了一段路程,又以4米/秒的速度跑完了其余的路程,一共花了10分钟,王强以6米秒的速度跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P,Q分别从A,B两点同时出发,在数轴上运动,它们的速度分别是2个单位长度/s、4个单位长度/s,它们运动的时间为t s.
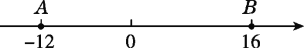
(1)如果点P,Q在点A,B之间相向运动,当它们相遇时,点P对应的数是________;
(2)如果点P,Q都向左运动,当点Q追上点P时,求点P对应的数;
(3)如果点P,Q在点A,B之间相向运动,当PQ=8时,求点P对应的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
①-3,9,-27,81,-243,729,…;
②0,12,-24,84,-240,732,…;
③-1,3,-9,27,-81,243,….
(1)第①行数有什么规律?
(2)第②行数与第①行数有什么关系?
(3)第③行数与第①行数有什么关系?
(4)取每行数的第10个数,计算这三个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
 的图象经过第二象限内的点A(
的图象经过第二象限内的点A(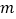 ,4),AB⊥x轴于点B,△AOB的面积为2,若直线
,4),AB⊥x轴于点B,△AOB的面积为2,若直线 经过点A,并且经过反比例函数
经过点A,并且经过反比例函数 的图象上另一点C(2,
的图象上另一点C(2,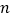 ).
).(1)求反比例函数和直线的解析式;
(2)设直线
 与
与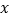 轴交于点M,求AM的长.
轴交于点M,求AM的长.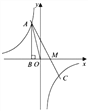
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

相关试题

