【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

参考答案:
【答案】证明见解析
【解析】试题分析:(1)利用平行四边形的性质得出∠5=∠3,∠AEB=∠4,进而利用全等三角形的判定得出即可;
(2)利用全等三角形的性质得出AE=CF,进而得出四边形AECF是平行四边形,即可得出答案.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,
 ,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;

(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列各题.
(1)先化简,再求值:
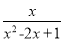 ÷
÷ ,其中x=
,其中x= +1.
+1.(2)分解因式:8(x2-2y2)-x(7x+y)+xy.
(3)解不等式
 ≤
≤ -1,并把解集表示在数轴上.
-1,并把解集表示在数轴上.
(4)解不等式组
 并将解集在数轴上表示出来.
并将解集在数轴上表示出来.
(5)解方程:
 +
+ =4.
=4. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买3台学习机多600元,购买2台平板电脑和3台学习机共需8400元.
(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168000元,且购买学习机的台数不超过购买平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)
 (2)
(2) 
(3)
 (4)
(4) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P的坐标(2a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(2,y)在第四象限,则y的取值范围是( )
A.y<0B.y>0
C.y大于或等于0D.y小于或等于0
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句正确的是( )
A.平角就是一条直线B.周角就是一条射线
C.小于平角的角是钝角D.一周角等于四个直角
相关试题

