【题目】如图1,已知面积为12的长方形ABCD,一边AB在数轴上。点A表示的数为—2,点B表示的数为1,动点P从点B出发,以每秒1个单位长度的速度沿数轴向左匀速运动,设点P运动时间为t(t>0)秒.

(1)长方形的边AD长为 单位长度;
(2)当三角形ADP面积为3时,求P点在数轴上表示的数是多少;
(3)如图2,若动点Q以每秒3个单位长度的速度,从点A沿数轴向右匀速运动,与P点出发时间相同。那么当三角形BDQ,三角形BPC两者面积之差为![]() 时,直接写出运动时间t 的值.
时,直接写出运动时间t 的值.
参考答案:
【答案】(1)4;(2)-3.5或-0.5;(3)t的值为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)先求出AB的长,由长方形ABCD的面积为12,即可求出AD的长;
(2)由三角形ADP面积为3,求出AP的长,然后分两种情况讨论:①点P在点A的左边;②点P在点A的右边.
(3) 分两种情况讨论:①若Q在B的左边,则BQ= 3-3t.由|S△BDQ-S△BPC |=![]() ,解方程即可;②若Q在B的右边,则BQ= 3t-3.由|S△BDQ-S△BPC |=
,解方程即可;②若Q在B的右边,则BQ= 3t-3.由|S△BDQ-S△BPC |=![]() ,解方程即可.
,解方程即可.
(1)AB=1-(-2)=3.
∵长方形ABCD的面积为12,∴AB×AD=12,∴AD=12÷3=4.
故答案为:4.
(2)三角形ADP面积为:![]() APAD=
APAD=![]() AP×4=3,
AP×4=3,
解得:AP=1.5,
点P在点A的左边:-2-1.5=-3.5,P 点在数轴上表示-3.5;
点P在点A的右边:-2+1.5=-0.5,P 点在数轴上表示-0.5.
综上所述:P 点在数轴上表示-3.5或-0.5.
(3)分两种情况讨论:①若Q在B的左边,则BQ=AB-AQ=3-3t.
S△BDQ=![]() BQAD=
BQAD=![]() =
=![]() ,S△BPC=
,S△BPC=![]() BPAD=
BPAD=![]() =
=![]() ,
,
![]() ,
,![]() ,解得:t=
,解得:t=![]() 或
或
②若Q在B的右边,则BQ=AQ-AB=3t-3.
S△BDQ=![]() BQAD=
BQAD=![]() =
=![]() ,S△BPC=
,S△BPC=![]() BPAD=
BPAD=![]() =
=![]() ,
,
![]() ,
,![]() ,解得:t=
,解得:t=![]() 或
或![]() .
.
综上所述:t的值为![]() 、
、![]() 、
、![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
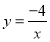 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 其图象分别位于第一、三象限
B. 当
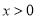 时,
时,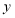 随
随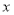 的增大而减小
的增大而减小C. 若点
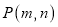 在它的图象上,则点
在它的图象上,则点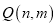 也在它的图象上
也在它的图象上D. 若点
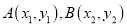 都在该函数图象上,且
都在该函数图象上,且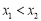 ,则
,则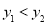
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
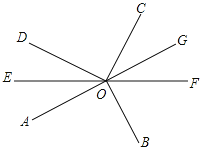
(1)∠AOD和∠BOC是否互补?说明理由;
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成了4:3的两个角,求∠AOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字,小明做了60次投掷试验,结果统计如下:
朝下数字
1
2
3
4
出现的次数
16
20
14
10
(1)求上述试验中“2朝下”的频率;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于5的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知轮船在静水中航行的速度是m千米/时,水流的速度是a千米/时.
(1)轮船顺水航行的速度为 km/h,轮船逆流航行的速度为 km/h.
(2)若轮船顺水航行3小时,逆水航行2小时,则轮船共航行多少千米?
(3)当m=80,a=3时,则轮船共航行多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为
 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图: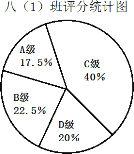

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分)
中位数(分)
众数(分)
八(1)班
83.75
80
八(2)班
80
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个足球垂直地面向上踢,
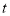 (秒)后该足球的高度
(秒)后该足球的高度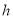 (米)适用公式
(米)适用公式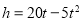 .
.(1)经多少秒时足球的高度为20米?
(2)小明同学说:“足球高度不可能达到21米!”你认为他说得对吗?请说明理由.
相关试题

