【题目】如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
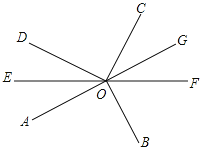
(1)∠AOD和∠BOC是否互补?说明理由;
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成了4:3的两个角,求∠AOD.
参考答案:
【答案】(1)互补;理由见解析;(2)是;理由见解析;(3)54°或![]()
【解析】
(1)根据和等于180°的两个角互补即可求解;
(2)通过求解得到∠COF=∠BOF,根据角平分线的定义即可得出结论;
(3)分两种情况:①当∠COG:∠GOF=4:3时;②当∠COG:∠GOF=3:4时;进行讨论即可求解.
(1)因为∠AOD+∠BOC=360°﹣∠AOB﹣∠DOC=360°﹣90°﹣90°=180°,
所以∠AOD和∠BOC互补.
(2)因为OE平分∠AOD,所以∠AOE=∠DOE,
因为∠COF=180°﹣∠DOC﹣∠DOE=90°﹣∠DOE,
∠BOF=180°﹣∠AOB﹣∠AOE=90°﹣∠AOE,
所以∠COF=∠BOF,即OF是∠BOC的平分线.
(3)因为OG将∠COF分成了4:3的两个部分,
所以∠COG:∠GOF=4:3或者∠COG:∠GOF=3:4.
①当∠COG:∠GOF=4:3时,设∠COG=4x°,则∠GOF=3x°,
由(2)得:∠BOF=∠COF=7x°
因为∠AOB+∠BOF+∠FOG=180°,
所以90°+7x+3x=180°,
解方程得:x=9°,
所以∠AOD=180°﹣∠BOC=180°﹣14x=54°.
②当∠COG:∠GOF=3:4时,设∠COG=3x°,∠GOF=4x°,
同理可列出方程:90°+7x+4x=180°,
解得:x = ![]() ,
,
所以∠AOD=180°﹣∠BOC=180°﹣14x![]() .
.
综上所述:∠AOD的度数是54°或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意及解答过程填空:
如图所示,AB=10cm,D为AC的中点,DC=2cm,BE=
 BC,求CE的长。
BC,求CE的长。
解:因为D为AC的中点,DC=2cm.
所以AC="_______DC=_______" cm.
由图可知:BC="______" -AC
="10" cm-____cm
=_______cm.
所以BE=
 BC=______cm.
BC=______cm.所以CE=BC-BE=_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,我们国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:

(1)根据上图填写下表:
平均数
中位数
众数
方差
甲班
8.5
乙班
8.5
10
1.6
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
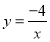 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 其图象分别位于第一、三象限
B. 当
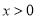 时,
时,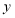 随
随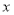 的增大而减小
的增大而减小C. 若点
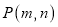 在它的图象上,则点
在它的图象上,则点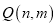 也在它的图象上
也在它的图象上D. 若点
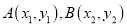 都在该函数图象上,且
都在该函数图象上,且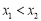 ,则
,则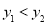
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字,小明做了60次投掷试验,结果统计如下:
朝下数字
1
2
3
4
出现的次数
16
20
14
10
(1)求上述试验中“2朝下”的频率;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于5的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知面积为12的长方形ABCD,一边AB在数轴上。点A表示的数为—2,点B表示的数为1,动点P从点B出发,以每秒1个单位长度的速度沿数轴向左匀速运动,设点P运动时间为t(t>0)秒.

(1)长方形的边AD长为 单位长度;
(2)当三角形ADP面积为3时,求P点在数轴上表示的数是多少;
(3)如图2,若动点Q以每秒3个单位长度的速度,从点A沿数轴向右匀速运动,与P点出发时间相同。那么当三角形BDQ,三角形BPC两者面积之差为
 时,直接写出运动时间t 的值.
时,直接写出运动时间t 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知轮船在静水中航行的速度是m千米/时,水流的速度是a千米/时.
(1)轮船顺水航行的速度为 km/h,轮船逆流航行的速度为 km/h.
(2)若轮船顺水航行3小时,逆水航行2小时,则轮船共航行多少千米?
(3)当m=80,a=3时,则轮船共航行多少千米?
相关试题

