【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上. 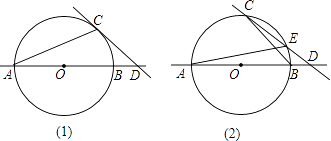
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次?
参考答案:
【答案】
(1)证明:如图(1),连接OC,
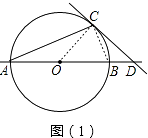
∵OA=OC,
∴∠OAC=∠OCA,
又∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠BCD=∠BAC=∠OCA,
∴∠BCD+∠OCB=90°,即OC⊥CD,
∴CD是⊙O的切线
(2)解:∵∠ADE=∠CDB,∠BCD=∠EAD,
∴△BCD∽△EAD,
∴ ![]() ,
,
∴ ![]() ,
,
又∵BD:DE:EC=2:3:5,⊙O的半径为5,
∴BD=2,DE=3,EC=5,
如图(2),连接OC、OE,则△OEC是等边三角形,
作OF⊥CE于F,则EF= ![]() CE=
CE= ![]() ,∴OF=
,∴OF= ![]() ,
,
∴圆心O到直线CD的距离是 ![]() .
.
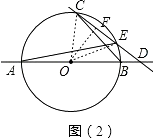
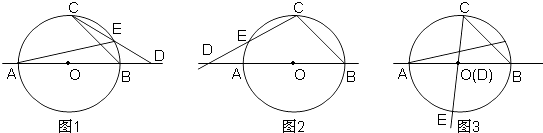
(3)解:这样的情形共有出现三次:
当点D在⊙O外时,点E是CD中点,有以下两种情形,如图1、图2;
当点D在⊙O内时,点D是CE中点,有以下一种情形,如图3.
【解析】(1)连接OC,根据弦切角定理和圆的性质可得到∠BCD=∠BAC=∠OCA,结合圆周角定理可求得∠OCD=90°,可证明CD是切线;(2)先证明△BCD∽△EAD,结合条件可求得BD=2,DE=3,EC=5,在△OBC中可求得O到CD的距离;(3)分点D在⊙O外和点D在⊙O内两种情况,当D在⊙O外时又分D在A点左边和D在B点右边两种情况,当D在⊙O内时只有一种,结合图形可给出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
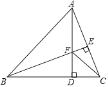
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别
成绩x(分数)
组中值
频数(人数)
1
90≤x<100
95
10
2
80≤x<90
85
25
3
70≤x<80
75
12
4
60≤x<70
65
3

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号
月租费(元)
免费时间(分)
超过免费时间的通话费(元/分)
一
10
0
0.20
二
30
80
0.15
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.
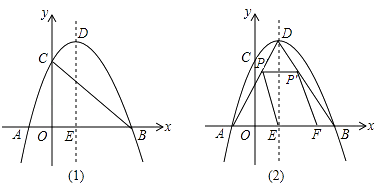
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①如果两个三角形全等,那么这两个三角形一定成轴对称;②数轴上的点和实数一一对应;③
 是3的一个平方根;④两个无理数的和一定为无理数;⑤6.9
是3的一个平方根;④两个无理数的和一定为无理数;⑤6.9 103精确到十分位;⑥
103精确到十分位;⑥ 的平方根是
的平方根是 4.其中正确的__________ .(填序号)
4.其中正确的__________ .(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )
A.
B.
C.
D.
相关试题

