【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号 | 月租费(元) | 免费时间(分) | 超过免费时间的通话费(元/分) |
一 | 10 | 0 | 0.20 |
二 | 30 | 80 | 0.15 |
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱.
参考答案:
【答案】
(1)解:方案一:y一=0.2x+10;
方案二:当0≤x≤80时,
y二=30.
当x>80时,
y二=0.15x+18,
∴y二= ![]()
(2)解:列表为:
x | 0 | 80 | 100 |
y一=0.2x+10 | 10 | 26 | |
y二=30(0≤x≤80) | 30 | 30 | |
y二=0.15x+18(x>80) | 30 | 33 |
描点并连线为:
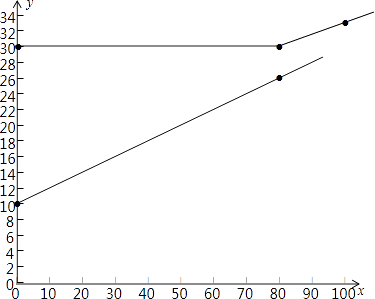
(3)解:当x=200时,
y一=10+0.2×200=50,
y二=0.15×200+18=48.
∵50>48,
∴方案二最省钱
【解析】(1)根据月话费=月租费+通话费就可以求出结论;(2)通过列表法就可以画出函数图象;(3)当x=200分别代入(1)的两个解析式就可以求出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别
成绩x(分数)
组中值
频数(人数)
1
90≤x<100
95
10
2
80≤x<90
85
25
3
70≤x<80
75
12
4
60≤x<70
65
3

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人. -
科目: 来源: 题型:
查看答案和解析>>【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量
房间价格
总维护费用
提价前
60
200
60×20
提价后
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
-
科目: 来源: 题型:
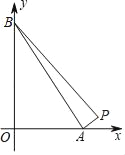
查看答案和解析>>【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
(1)如图,若0<a<14,求a的值.
(2)如果a>14,请画图并求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上.
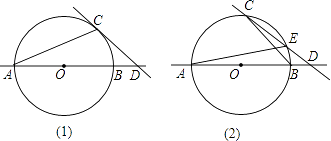
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
(1)若折叠后使点B与点A重合,求点C的坐标.
(2)若折叠后点B落在边OA上的点为B′,是否存在点B′,使得四边形BCB′D是菱形?若存在,请说明理由并求出菱形的边长;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.

(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
相关试题

