【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
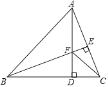
A. 0个 B. 1个 C. 2个 D. 3个
参考答案:
【答案】D
【解析】
证明△ADC≌△BDF即可一一判断.
解:∵△ABC中,AD,BE分别为BC、AC边上的高,∠ABC=45°,
∴AD=BD,∠DAC和∠FBD都是∠ACD的余角,
而∠ADB=∠ADC=90°,
∴△BDF≌△ADC,
∴BF=AC,故①正确,
∴FD=CD,
∴∠FCD=∠CFD=45°,故②正确;
若BF=2EC,根据①得BF=AC,
∴AC=2EC,
即E为AC的中点,
∴BE为线段AC的垂直平分线,
∴AF=CF,BA=BC,
∴AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD,
即△FDC周长等于AB的长,故③正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣4|﹣22+
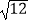 ﹣tan60°(说明:本题不允许使用计算器计算)
﹣tan60°(说明:本题不允许使用计算器计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
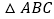 和
和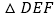 是两个全等的三角形,
是两个全等的三角形,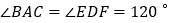 ,
,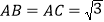 .现将
.现将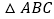 和
和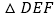 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,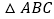 保持不动,
保持不动,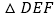 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在
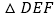 的运动过程中,
的运动过程中,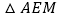 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.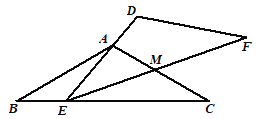
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是BC的中点.
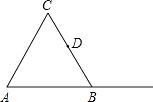
(1)作图: ①过B作AC的平行线BH;
②过D作BH的垂线,分别交AC,BH,AB的延长线于E,F,G.
(2)在图中找出一对全等的三角形,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别
成绩x(分数)
组中值
频数(人数)
1
90≤x<100
95
10
2
80≤x<90
85
25
3
70≤x<80
75
12
4
60≤x<70
65
3

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号
月租费(元)
免费时间(分)
超过免费时间的通话费(元/分)
一
10
0
0.20
二
30
80
0.15
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱. -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上.
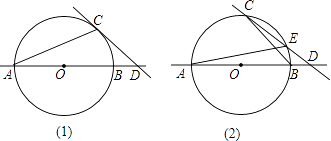
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次?
相关试题

