【题目】完成下面推理过程:
如图,已知![]() ,可推得
,可推得![]() ,理由如下:
,理由如下:
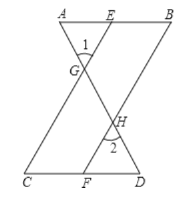
![]() ( )
( )
且![]() ( )
( )
![]() (等量代换)
(等量代换)
![]() ( )
( )
∴∠ =∠C( ).
又![]() (已知),
(已知),
![]()
![]() ( )
( )
![]() ( )
( )
参考答案:
【答案】已知;对顶角相等;同位角相等,两直线平行;BFD;两直线平行,同位角相等;BFD;等量代换;内错角相等,两直线平行.
【解析】
先确定∠1=∠CGD是对顶角,利用等量代换,求得∠2=∠CGD,则可根据:同位角相等,两直线平行,证得:CE∥BF,又由两直线平行,同位角相等,证得角相等,易得:∠BFD=∠B,则利用内错角相等,两直线平行,即可证得:AB∥CD.
解:∵∠1=∠2 (已知),且∠1=∠CGD(对顶角相等),
∴∠2=∠CGD (等量代换),
∴CE∥BF(同位角相等,两直线平行).
∴∠BFD=∠C(两直线平行,同位角相等).
又∵∠B=∠C (已知),
∴∠BFD=∠B (等量代换),
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知;对顶角相等;同位角相等,两直线平行;BFD;两直线平行,同位角相等;BFD;等量代换;内错角相等,两直线平行.
-
科目: 来源: 题型:
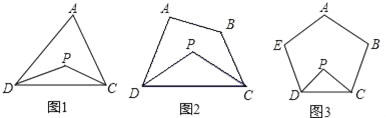
查看答案和解析>>【题目】(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD,如果∠A=90°,那么∠P=______°;如果∠A=x°,则∠P=____________°;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E的数量关系:________________;
(4)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:__________________________.(用含n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与点C重合,折痕EF交AD于点E,交BC于点F,交AC于点O,连结AF,CE.
(1)求证:四边形AFCE是菱形;
(2)若AE=8,△ABF的面积为9,求AB+BF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
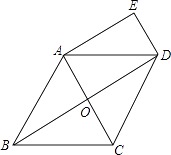
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径

(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.

(1)求证:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:
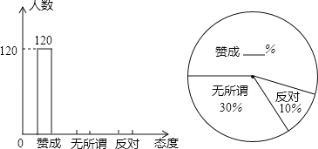
根据上述信息,解答下列问题:
(1)抽取的学生人数为 ;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
相关试题

