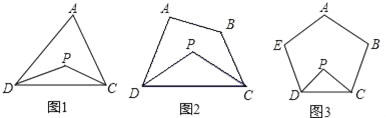
【题目】(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD,如果∠A=90°,那么∠P=______°;如果∠A=x°,则∠P=____________°;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E的数量关系:________________;
(4)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:__________________________.(用含n的代数式表示)
参考答案:
【答案】如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+![]() )° ∠P=
)° ∠P=![]() (∠A+∠B) ∠P=
(∠A+∠B) ∠P=![]() (∠A+∠B+∠E)﹣90° ∠P=
(∠A+∠B+∠E)﹣90° ∠P=![]() (∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°
(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°
【解析】
(1)根据角平分线的定义和三角形内角和定理,列式整理解答;
(2)根据角平分线的定义和四边形的内角和,列式整理解答;
(3)根据角平分线的定义和五边形的内角和,列式整理解答;
(4)根据角平分线的定义和n边形的内角和公式,列式整理解答;
(1)∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD
∠ACD
=180°﹣![]() (∠ADC+∠ACD)
(∠ADC+∠ACD)
=180°﹣![]() (180°﹣∠A)
(180°﹣∠A)
=90°+ ![]() ∠A,
∠A,
∴如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+![]() )°;
)°;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD
∠BCD
=180°﹣![]() (∠ADC+∠BCD)
(∠ADC+∠BCD)
=180°﹣![]() (360°﹣∠A﹣∠B)
(360°﹣∠A﹣∠B)
![]() (∠A+∠B);
(∠A+∠B);
(3)五边形ABCDEF的内角和为:(5﹣2)180°=540°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=![]() ∠EDC,∠PCD=
∠EDC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠EDC﹣
∠EDC﹣![]() ∠BCD
∠BCD
=180°﹣![]() (∠EDC+∠BCD)
(∠EDC+∠BCD)
=180°﹣![]() (540°﹣∠A﹣∠B﹣∠E)
(540°﹣∠A﹣∠B﹣∠E)
=![]() (∠A+∠B+∠E)﹣90°,
(∠A+∠B+∠E)﹣90°,
即∠P=![]() (∠A+∠B+∠E)﹣90°;
(∠A+∠B+∠E)﹣90°;
(4)同(1)可得,∠P=![]() (∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
故答案为:(1)如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+![]() )°(2)∠P=180°﹣∠PDC﹣∠PCD=
)°(2)∠P=180°﹣∠PDC﹣∠PCD=![]() (∠A+∠B)(3)∠P=
(∠A+∠B)(3)∠P=![]() (∠A+∠B+∠E)﹣90°(4)∠P=
(∠A+∠B+∠E)﹣90°(4)∠P=![]() (∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°
(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°
-
科目: 来源: 题型:
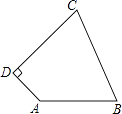
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
-
科目: 来源: 题型:
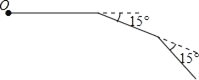
查看答案和解析>>【题目】如图,小明从点O出发,前进5m后向右转15°,再前进5m后又向右转15°,…这样一直下去,直到他第一次回到出发点O为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).
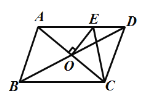
A. 8cm B. 10cm C. 11cm D. 12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与点C重合,折痕EF交AD于点E,交BC于点F,交AC于点O,连结AF,CE.
(1)求证:四边形AFCE是菱形;
(2)若AE=8,△ABF的面积为9,求AB+BF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
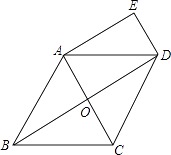
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知
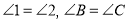 ,可推得
,可推得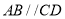 ,理由如下:
,理由如下: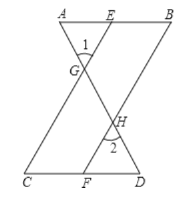
 ( )
( )且
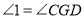 ( )
( )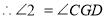 (等量代换)
(等量代换)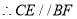 ( )
( )∴∠ =∠C( ).
又
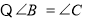 (已知),
(已知),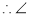
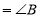 ( )
( )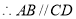 ( )
( )
相关试题

