搜索
【题目】已知如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．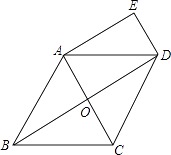
（1）求证：四边形AODE是矩形；
（2）若AB=6，∠BCD=120°，求四边形AODE的面积．
参考答案：
【答案】
（1）证明：∵DE∥AC，AE∥BD，
∴四边形AODE是平行四边形，
∵在菱形ABCD中，AC⊥BD，
∴∠AOD=90°，
∴四边形AODE是矩形；
（2）解：∵∠BCD=120°，AB∥CD，
∴∠ABC=180°﹣120°=60°，
∵AB=BC，
∴△ABC是等边三角形，
∴OA= 
×6=3，OB= 
×6=3 
，
∵四边形ABCD是菱形，
∴OD=OB=3 ，
∴四边形AODE的面积=OAOD=3×3 =9 ．
【解析】（1）由已知DE∥AC，AE∥BD，可证得四边形AODE是平行四边形，再证明有一个角是直角，由菱形ABCD，即可证出∠AOD是直角，即可证得结论。
（2）抓住已知∠BCD=120°，根据菱形的性质证明△ABC是等边三角形，再利用勾股定理求出OA、OD的长，即可求出矩形AODE的面积。
-
科目： 来源： 题型：
查看答案和解析>>【题目】在□ABCD中，O是AC、BD的交点，过点O 与AC垂直的直线交边AD于点E，若□ABCD的周长为22cm，则△CDE的周长为（ ）．
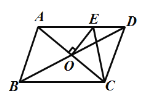
A. 8cm B. 10cm C. 11cm D. 12cm
-
科目： 来源： 题型：
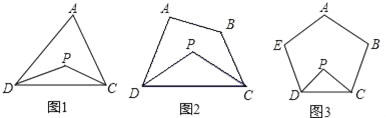
查看答案和解析>>【题目】（1）已知：如图1，P为△ADC内一点，DP、CP分别平分∠ADC和∠ACD，如果∠A=90°，那么∠P=______°；如果∠A=x°，则∠P=____________°；（答案直接填在题中横线上）
（2）如图2，P为四边形ABCD内一点，DP、CP分别平分∠ADC和∠BCD，试探究∠P与∠A+∠B的数量关系，并写出你的探索过程；
（3）如图3，P为五边形ABCDE内一点，DP、CP分别平分∠EDC和∠BCD，请直接写出∠P与∠A+∠B+∠E的数量关系：________________；
（4）若P为n边形A1A2A3…An内一点，PA1平分∠AnA1A2，PA2平分∠A1A2A3，请直接写出∠P与∠A3+A4+A5+…∠An的数量关系：__________________________．（用含n的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形纸片ABCD（AD＞AB）中，将它折叠，使点A与点C重合，折痕EF交AD于点E，交BC于点F，交AC于点O，连结AF，CE.
（1）求证：四边形AFCE是菱形；
（2）若AE＝8，△ABF的面积为9，求AB＋BF的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面推理过程：
如图，已知
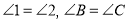，可推得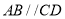
，理由如下：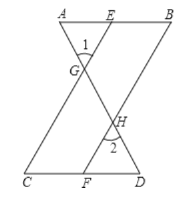
( )且
( )
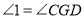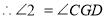(等量代换)
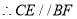（ ）∴∠ =∠C（ ）．
又
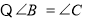(已知)，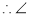
（ ）
（ ） -
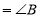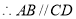科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知等腰直角△ABC，点P是斜边BC上一点（不与B，C重合），PE是△ABP的外接圆⊙O的直径
（1）求证：△APE是等腰直角三角形；
（2）若⊙O的直径为2，求
的值 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC和△DBC中，∠ACB=∠DBC=90°，点E是BC的中点，EF⊥AB，垂足为F，且AB=DE．
（1）求证：△BCD是等腰直角三角形；
（2）若BD=8厘米，求AC的长．
相关试题
