【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从八、九两个年级各随机抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
八年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
九年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按如下分数段整理、描述这两组样本数据:
|
|
|
|
|
| |
八年级 | 0 | 0 | 1 | 11 | 1 | |
九年级 | 1 | 0 | 0 | 7 |
(说明:成绩![]() 分及以上为体质健康优秀,
分及以上为体质健康优秀,![]() ~
~![]() 分为体质健康良好,
分为体质健康良好,![]() ~
~![]() 分为体质健康合格,
分为体质健康合格,![]() 分以下为体质健康不合格)
分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 |
|
|
| 33.6 |
九年级 |
|
| 52.1 |
请将以上两个表格补充完整;
得出结论
(1)估计九年级体质健康优秀的学生人数为__________;
(2)可以推断出_______年级学生的体质健康情况更好一些,理由为_________________.(至少从两个不同的角度说明推断的合理性).
参考答案:
【答案】(1)108;(2)答案不唯一,理由需支撑推断结即可
【解析】(1)对原始数据进行整理可得;(2)用样本情况估计总体情况;从平均数和方差分析整体情况.
分析各年级数据,可知:八班级![]() 有7人,九年级有10人;九年级
有7人,九年级有10人;九年级![]() 有2人;九年级81分出现次数4,最多,所以众数是81;(1)估计九年级体质健康优秀的学生人数为:
有2人;九年级81分出现次数4,最多,所以众数是81;(1)估计九年级体质健康优秀的学生人数为:![]() 人;(2)可以推断出八年级学生的体质健康情况更好一些,理由为:九年级平均分上比八年级少,同时八班级方差较小,说明比较稳定于良好水平.
人;(2)可以推断出八年级学生的体质健康情况更好一些,理由为:九年级平均分上比八年级少,同时八班级方差较小,说明比较稳定于良好水平.
-
科目: 来源: 题型:
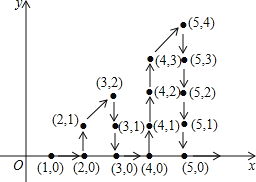
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第2019个点的坐标为_____.
-
科目: 来源: 题型:
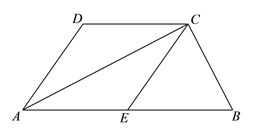
查看答案和解析>>【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
-
科目: 来源: 题型:
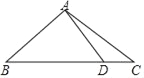
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为__________________元(用含a的代数式表示);
当x≥16时,支付费用为_________________元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
物品重量(千克)
支付费用(元)
18
39
25
53
试根据以上提供的信息确定a,b的值.
(3)根据这个规定,若丙要托运一件超过16千克的物品,但支付的费用不想超过70元,那么丙托运的物品最多是多少千克.
相关试题

