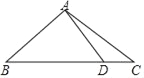
【题目】如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
参考答案:
【答案】(1)60°;(2)6.
【解析】
(1)由题意可得∠B=∠C=30°,由AB⊥AD,可求∠BDA的度数;
(2)根据30度所对的直角边等于斜边的一半,可求BD=4,根据三角形的外角等于不相邻的两个内角和,可求∠C=∠DAC=30°,可得AD=CD=2,即可求BC的长.
解:(1)∵AB=AC,
∴∠B=∠C=30°,
∵AD⊥AB,
∴∠BDA+∠B=90°,
∴∠BDA=60°;
(2)∵∠BDA=60°,∠C=30°,且∠BDA=∠C+∠DAC,
∴∠DAC=60°﹣30°=30°=∠C,
∴AD=CD=2,
∵AB⊥AD,∠B=30°,
∴BD=2AD=4,
∵BC=BD+CD,
∴BC=2+4=6.
-
科目: 来源: 题型:
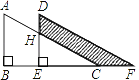
查看答案和解析>>【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
-
科目: 来源: 题型:
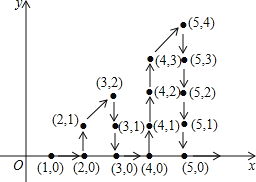
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第2019个点的坐标为_____.
-
科目: 来源: 题型:
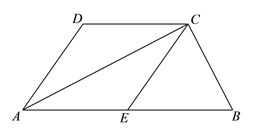
查看答案和解析>>【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从八、九两个年级各随机抽取
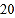 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:八年级
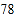
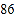
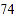


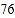
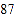


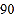




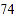
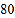
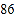
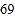
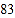
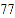
九年级

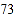




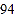
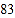
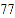
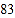
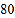



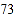
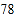

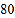

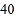
整理、描述数据
按如下分数段整理、描述这两组样本数据:
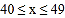

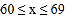
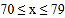
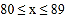
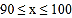
八年级
0
0
1
11
1
九年级
1
0
0
7
(说明:成绩
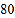 分及以上为体质健康优秀,
分及以上为体质健康优秀, ~
~ 分为体质健康良好,
分为体质健康良好,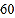 ~
~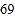 分为体质健康合格,
分为体质健康合格,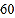 分以下为体质健康不合格)
分以下为体质健康不合格)分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
八年级
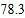
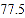

33.6
九年级
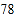
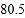
52.1
请将以上两个表格补充完整;
得出结论
(1)估计九年级体质健康优秀的学生人数为__________;
(2)可以推断出_______年级学生的体质健康情况更好一些,理由为_________________.(至少从两个不同的角度说明推断的合理性).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
相关试题

