【题目】如图,直线![]() ,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做
,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做![]() ,使
,使![]() ,设
,设![]() ,
,![]() 的平分线所在直线交PQ于点D.
的平分线所在直线交PQ于点D.
(1)如图1,若![]() ,且点C恰好落在直线MN上,则
,且点C恰好落在直线MN上,则![]() ________;
________;
(2)如图2,若![]() ,且点C在直线MN右侧,求
,且点C在直线MN右侧,求![]() 的度数;
的度数;
(3)若点C在直线MN的左侧,求![]() 的度数.(用含有α的式子表示)
的度数.(用含有α的式子表示)

参考答案:
【答案】(1)45o;(2) 45o;(3) ![]() .
.
【解析】
(1)证明△ADB是等腰直角三角形即可解决问题.
(2)如图2中,设![]() ,
,![]() .构建方程组即可解决问题.
.构建方程组即可解决问题.
(3)分两种情形:①当点C在直线PQ与MN之间时,设![]() ,
,![]() .②当点C在直线PQ左边时,设
.②当点C在直线PQ左边时,设![]() ,
,![]() .利用平行线的性质、三角形内角和定理、三角形外角性质、四边形内角和定理分别构建方程组即可解决问题.
.利用平行线的性质、三角形内角和定理、三角形外角性质、四边形内角和定理分别构建方程组即可解决问题.
解:(1)如图1中,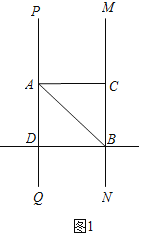
∵PQ∥MN,
∴∠ACB+∠CAD=180°,
∵∠ACB=90°,
∴∠CAD=90°,
∵∠BAC=∠BAQ,
∴∠BAD=45°,
∵DB平分∠CBN,
∴∠DBC=90°,
∵PQ∥MN,
∴∠ADB=90°,
∴∠ABD=45°.
故答案为45°.
(2)根据题意,如图所示,设![]() ,
,![]()
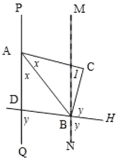
∵![]()
∴![]() ,
, ![]()
∵![]()
∵![]()
∴![]()
∴![]()
(3)①根据题意,如图所示,设![]() ,
,![]()
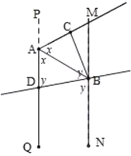
∵![]()
∴![]()
∵![]()
由四边形内角和为![]()
可得![]()
∴![]()
∴![]()
∴![]()
②根据题意,如图所示,设![]() ,
,![]()
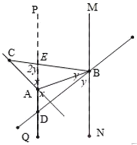
∵![]()
∴![]()
![]()
![]()
在![]() 中
中![]()
![]()
∴![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线.
(2)若AB=2
 ,求OC的长.
,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求
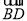 的长(结果保留π).
的长(结果保留π).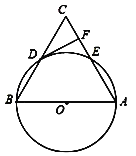
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________,
 =________%,
=________%,  =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=
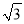 ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作 ,交OB于E点.
,交OB于E点.(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

-
科目: 来源: 题型:
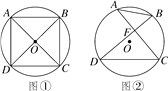
查看答案和解析>>【题目】已知A,B,C,D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图②,若AC⊥BD,垂足为F,AB=2,DC=4,求⊙O的半径.
相关试题

