【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

参考答案:
【答案】(1)⊙O的半径OA的长为2;(2)阴影部分的面积为![]() .
.
【解析】试题分析: ![]() 连接OD.首先证明∠OCD=90°.构造直角三角形,运用勾股定理列出方程求解即可.
连接OD.首先证明∠OCD=90°.构造直角三角形,运用勾股定理列出方程求解即可.
![]() S阴影=S△CDO+S扇形OBD-S扇形OCE.
S阴影=S△CDO+S扇形OBD-S扇形OCE.
试题解析:(1)连接OD.∵OA⊥OB,
∴∠AOB=90°.
∵CD∥OB,
∴∠OCD=90°.
在Rt△OCD中,∵C是AO的中点, ![]()
∴OD=2OC.
设OC=x, ![]()
∴x=1,∴OD=2,
∴⊙O的半径为2;
(2) ![]()
∴∠CDO=30°.
∵FD∥OB,
∴∠DOB=∠CDO=30°,
∴S阴影=S△CDO+S扇形OBD-S扇形OCE![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2+2a+1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m2﹣m)x2+(m﹣1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应怎样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣
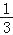 x+1与y轴交于点D.
x+1与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
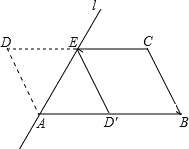
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2的图象向右平移2个单位,得到新的函数图像的表达式是( )
A. y=x2-2 B. y=(x-2)2 C. y=x2+2 D. y=(x+2)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的顶点坐标为(1,4),且其图象经过点(-2,-5),求此二次函数的解析式。
相关试题

