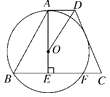
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)过点O作OG⊥DC,垂足为G.先证明∠OAD=90°,从而得到∠OAD=∠OGD=90°,然后利用AAS可证明△ADO≌△GDO,则OA=OG=r,则DC是⊙O的切线;
(2)连接OF,依据垂径定理可知BE=EF=12,在Rt△OEF中,依据勾股定理可知求得OF=13,然后可得到AE的长,最后在Rt△ABE中,利用锐角三角函数的定义求解即可.
试题解析:
(1)证明:
过点O作OG⊥DC,垂足为G.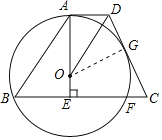
∵AD∥BC,AE⊥BC于E,
∴OA⊥AD.
∴∠OAD=∠OGD=90°.
在△ADO和△GDO中
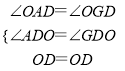 ,
,
∴△ADO≌△GDO.
∴OA=OG.
∴DC是⊙O的切线.
(2)如图所示:连接OF.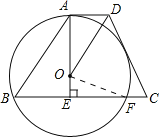
∵OA⊥BC,
∴BE=EF=![]() BF=12.
BF=12.
在Rt△OEF中,OE=5,EF=12,
∴OF=![]() ,
,
∴AE=OA+OE=13+5=18.
∴tan∠ABC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师所在的学校为加强学生的体育锻炼,需要购买若干个足球和篮球,他曾两次在某商场购买过足球和篮球,两次购买足球和篮球的数量和费用如下表:
足球数量(个)
篮球数量(个)
总费用(元)
第一次
3
5
550
第二次
6
7
860
(1)求足球和篮球的标价;
(2)陈老师计划购买足球a个,篮球b个,可用资金最高为4000元;
①如果计划购买足球和篮球共60个,最多购买篮球多少个?
②如果可用资金恰好全部用完,且购买足球数量不超过篮球数量,则陈老师最多可购买足球________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线.
(2)若AB=2
 ,求OC的长.
,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求
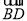 的长(结果保留π).
的长(结果保留π).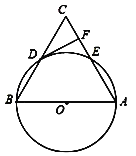
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 ,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做
,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做 ,使
,使 ,设
,设 ,
, 的平分线所在直线交PQ于点D.
的平分线所在直线交PQ于点D.(1)如图1,若
 ,且点C恰好落在直线MN上,则
,且点C恰好落在直线MN上,则 ________;
________;(2)如图2,若
 ,且点C在直线MN右侧,求
,且点C在直线MN右侧,求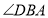 的度数;
的度数;(3)若点C在直线MN的左侧,求
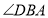 的度数.(用含有α的式子表示)
的度数.(用含有α的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________,
 =________%,
=________%,  =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=
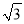 ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作 ,交OB于E点.
,交OB于E点.(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

相关试题

