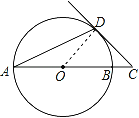
【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线.
(2)若AB=2![]() ,求OC的长.
,求OC的长.

参考答案:
【答案】(1)、证明过程见解析;(2)、2.
【解析】
试题分析:(1)、连接DO,由三角形的外角与内角的关系易得∠DOC=∠C=45°,故有∠ODC=90°,即CD是圆的切线.(2)、由1知,CD=OD=![]() AB,在直角△COD中,利用勾股定理即可求解.
AB,在直角△COD中,利用勾股定理即可求解.
试题解析:(1)、连接DO, ∵AO=DO, ∴∠DAO=∠ADO=22.5°. ∴∠DOC=45°.
又∵∠ACD=2∠DAB, ∴∠ACD=∠DOC=45°. ∴∠ODC=90°. 又∵OD是⊙O的半径,
∴CD是⊙O的切线.
(2)、连接DB, ∵直径AB=2![]() ,△OCD为等腰直角三角形, ∴CD=OD=
,△OCD为等腰直角三角形, ∴CD=OD=![]() ,OC=2.
,OC=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个数中,正整数是( )
A.﹣2
B.﹣1
C.0
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两个仓库要向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两库到A,B两地的路程和运费如下表(表中运费栏“元/(吨、千米)”表示每吨水泥运送1千米所需人民币)(本题满分10分)
路程/千米
运费(元/吨、千米)
甲库
乙库
甲库
乙库
A地
20
15
12
12
B地
25
20
10
8
(1)设甲库运往A地水泥
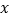 吨,求总运费
吨,求总运费 (元)关于
(元)关于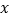 (吨)的函数关系式;
(吨)的函数关系式;(2)当甲、乙两库各运往A、B两地多少吨水泥时,总运费最省?最省的总运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x)2的结果是( )
A.2x2B.﹣2x2C.4x2D.﹣4x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.
(1)在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校初三400名学生的体重情况,从中抽取50名学生的体重进行分析.在这项调查中,下列说法正确的是( )
A.400名学生中每位学生是个体
B.400名学生是总体
C.被抽取的50名学生是总体的一个样本
D.样本的容量是50
相关试题

