Question

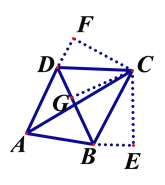
【题目】如图，在四边形ABCD中，对角线AC平分∠DAB，∠ABD=52°，∠ABC=116°，∠ACB=α°，则∠BDC的度数为（　　）

A. α B. α C. 90﹣α D. 90﹣α

Answer 1

【答案】C

【解析】分析：作CE⊥AB交AB的延长线于点E，作CF⊥AD交AD的延长线于点F，作CG⊥AB交BD于点G，由“AAS”证明△CBE≌△CBG，再由“HL”证明△CDG≌△CDF，得到∠CDG=∠CDF，由三角形内角和、外角和表示出∠FDB,进而可求出∠BDC的度数.

详解：作CE⊥AB交AB的延长线于点E，作CF⊥AD交AD的延长线于点F，作CG⊥AB交BD于点G.

∵∠ABD=52°，∠ABC=116°，

∴∠CBE=180-116=64, ∠CBD=116-52=64,

∴∠CBE=∠CBD.

在△CBE和△CBG中，

∵∠CBE=∠CBD，

∠E=∠CGB=90，

BC=BC，

∴△CBE≌△CBG，

∴CE=CG.

∵AC平分∠DAB，CG⊥AB，CE⊥AB，

∴CE=CF，

∴CG=CF.

在△CDG和△△CDF中，

∵CG=CF，

CD=CD，

∴△CDG≌△CDF，

∴∠CDG=∠CDF.

∵∠ABC=116°，∠ACB=α°，

∴∠CAB=180-116-α=64 -α,

∵AC平分∠DAB，

∴∠DAB=2(64 -α)=128-2α,

∴∠FDB=128-2α+52=180-2α,

∴∠BDC=(180+2α)=90-α.

故选C.