【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
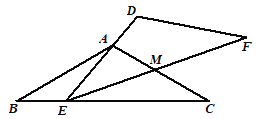
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
参考答案:
【答案】(1)证明见解析;(2)见解析;(3)见解析.
【解析】
(1)已知△ABC≌△DEF,根据全等三角形的性质可得∠ABC=∠DEF,又因∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC,即可得∠B+∠BAE=∠AEM+∠MEC,所以∠BAE=∠MEC;(2)当E为BC中点时, AB=AC,根据等腰三角形三线合一的性质可得AE⊥BC,∠EAM=60°,再由∠DEM=30°即可证得AC⊥EF; 在Rt△ABE中,∠B=30°,![]() ,求得BE=
,求得BE=![]() ,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=
,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=![]() E,求得EM=
E,求得EM=![]() ,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=
,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=![]() ,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、
,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、![]() 三种情况求解即可.
三种情况求解即可.
(1)证明:∵△ABC≌△DEF
∴∠ABC=∠DEF
∵∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC;
∴∠B+∠BAE=∠AEM+∠MEC,
即∠BAE=∠MEC ;
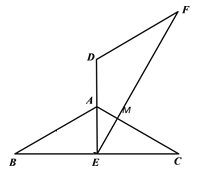
(2)当E为BC中点时,
∵AB=AC,
∴AE⊥BC,BE=EC=![]() ,∠EAM=60°,
,∠EAM=60°,
又∵∠DEM=30°,
∴AC⊥EF;
∵![]() ,
,![]() ,
,
∴∠B=∠C=30°,
在Rt△ABE中,∠B=30°,![]() ,
,
∴BE=![]() ,
,
∴BC=3;
在Rt△CEM中,∠C=30°,EC=![]() ,
,
∴EM=![]() ,
,
∵△ABC≌△DEF,
∴BC=EF=3,
∴FM= EF-EM=![]() ,
,
∴EM:FM=1:3;
(3)当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.
①当![]() 时,如图,
时,如图,

![]()
![]() ,
,
此时点E与点B重合,与题意矛盾(舍去 ) ;
②当![]() 时,如图,
时,如图,
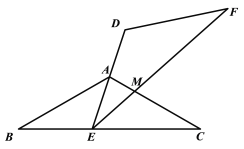
由(1)知,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
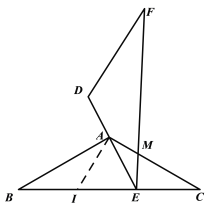
③当![]() 时,如图,
时,如图,
则![]() ,
,
![]() ,
,
取BE中点I,连结AI,
则![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
设![]() ,在
,在![]() 中,
中,
由勾股定理,得![]() ,
,
即![]() ,解得
,解得![]()
![]() .
.
综上所述,当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
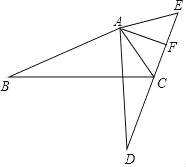
查看答案和解析>>【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BA=BC,BE平分∠ABC,CD⊥BD,且CD=BD.
(1)求证:BF=AC;
(2)若AD=
 ,求CF的长.
,求CF的长.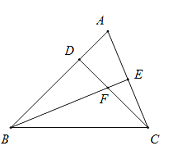
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣4|﹣22+
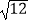 ﹣tan60°(说明:本题不允许使用计算器计算)
﹣tan60°(说明:本题不允许使用计算器计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是BC的中点.
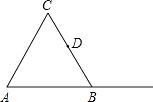
(1)作图: ①过B作AC的平行线BH;
②过D作BH的垂线,分别交AC,BH,AB的延长线于E,F,G.
(2)在图中找出一对全等的三角形,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
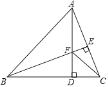
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别
成绩x(分数)
组中值
频数(人数)
1
90≤x<100
95
10
2
80≤x<90
85
25
3
70≤x<80
75
12
4
60≤x<70
65
3

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.
相关试题

