【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
(1)求证:AB是⊙O的切线;
(2)若∠A=60°,DF= ![]() ,求⊙O的直径BC的长.
,求⊙O的直径BC的长.
参考答案:
【答案】
(1)
证明:∵CD=CB,
∴∠CBD=∠CDB,
∵AB是⊙O的直径,
∴∠CBE=90°,
∴∠CBD+∠BCE=∠CDB+∠DCE,
∴∠BCE=∠DCE,
即∠BCD=2∠BCE,
∵∠BCD=2∠ABD,
∴∠ABD=∠BCE,
∴∠CBD+∠ABD=∠CBD+∠BCE=90°,
∴CB⊥AB,
∵CB为直径,
∴AB是⊙O的切线
(2)
解:∵∠A=60°,DF= ![]() ,
,
∴在Rt△AFD中,AF= ![]() =
= ![]() =1,
=1,
在Rt△BFD中,BF=DFtan60°= ![]() ×
× ![]() =3,
=3,
∵DF⊥AB,CB⊥AB,
∴DF∥BC,
∴∠ADF=∠ACB,
∵∠A=∠A,
∴△ADF∽△ACB,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CB=4 ![]() .
.
【解析】此题考查了切线的判定、等腰三角形的性质以及相似三角形的判定与性质.注意证得△ADF∽△ACB是解此题的关键.
(1)由CD=CB,∠BCD=2∠ABD,可证得∠BCE=∠ABD,继而求得∠ABC=90°,则可证得AB是⊙O的切线;(2)由∠A=60°,DF= ![]() ,可求得AF、BF的长,易证得△ADF∽△ACB,然后由相似三角形的对应边成比例,求得答案.
,可求得AF、BF的长,易证得△ADF∽△ACB,然后由相似三角形的对应边成比例,求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.

(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 = ___________;(2)
= ___________;(2) =___________;(3)
=___________;(3) =___________;(4)
=___________;(4) =________;(5)
=________;(5) __________;(6)
__________;(6) =___;(7)
=___;(7) _____;(8)
_____;(8) =__________.
=__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个两位数恰等于它的各位数字之和的
 倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个.
倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx与直线y=2x+4交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作x轴、y轴的平行线与直线AB交于点C和点E.
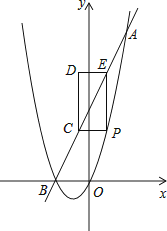
(1)求抛物线的解析式;
(2)若C为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
回答下列问题:
(1)这
 筐白菜中,最接近
筐白菜中,最接近 千克的那筐白菜为 千克;
千克的那筐白菜为 千克;(2)若白菜每千克售价
 元,则出售这8筐白菜可卖多少元?
元,则出售这8筐白菜可卖多少元?
相关试题

