【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
参考答案:
【答案】
(1)
证明:由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,
在△AEC和△ADB中,
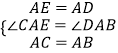 ,
,
∴△AEC≌△ADB(SAS);
(2)
解:∵四边形ADFC是菱形,且∠BAC=45°,
∴∠DBA=∠BAC=45°,
由(1)得:AB=AD,
∴∠DBA=∠BDA=45°,
∴△ABD为直角边为2的等腰直角三角形,
∴BD2=2AB2,即BD=2 ![]() ,
,
∴AD=DF=FC=AC=AB=2,
∴BF=BD﹣DF=2 ![]() ﹣2
﹣2
【解析】(1)由旋转的性质得到三角形ABC与三角形ADE全等,以及AB=AC,利用全等三角形对应边相等,对应角相等得到两对边相等,一对角相等,利用SAS得到三角形AEC与三角形ADB全等即可;
(2)根据∠BAC=45°,四边形ADFC是菱形,得到∠DBA=∠BAC=45°,再由AB=AD,得到三角形ABD为等腰直角三角形,求出BD的长,由BD﹣DF求出BF的长即可.此题考查了旋转的性质,全等三角形的判定与性质,以及菱形的性质,熟练掌握旋转的性质是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
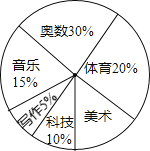
学习小组
体育
美术
科技
音乐
写作
奥数
人数
72
36
54
18
(1)七年级共有学生 人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是 ;
(4)众数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】OC把∠AOB分成两部分且有下列两个等式成立:
①∠AOC=
 直角+
直角+ ∠BOC;②∠BOC=
∠BOC;②∠BOC= 平角-
平角- ∠AOC,问∶
∠AOC,问∶(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点,已知OE=
 ,EF=3,求菱形ABCD的周长和面积.
,EF=3,求菱形ABCD的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.

(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 = ___________;(2)
= ___________;(2) =___________;(3)
=___________;(3) =___________;(4)
=___________;(4) =________;(5)
=________;(5) __________;(6)
__________;(6) =___;(7)
=___;(7) _____;(8)
_____;(8) =__________.
=__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.

(1)求证:AB是⊙O的切线;
(2)若∠A=60°,DF=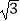 ,求⊙O的直径BC的长.
,求⊙O的直径BC的长.
相关试题

