【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

回答下列问题:
(1)这![]() 筐白菜中,最接近
筐白菜中,最接近![]() 千克的那筐白菜为 千克;
千克的那筐白菜为 千克;
(2)若白菜每千克售价![]() 元,则出售这8筐白菜可卖多少元?
元,则出售这8筐白菜可卖多少元?
参考答案:
【答案】(1)这8筐白菜中,最接近25千克标准的是第4筐,重24.5千克;(2)出售这8筐白菜可卖505.7元.
【解析】
(1)与标准重量比较,绝对值越小的越接近标准重量;
(2)白菜每千克售价2.6元,再计算出8筐白菜的总重量即可求出出售这8筐白菜可卖多少元.
解:(1)该组数据中,-0.5的绝对值最小,最接近25千克的标准,是第4筐,
这筐白菜重25-0.5=24.5千克.
答:这8筐白菜中,最接近25千克标准的是第4筐,重24.5千克;
(2)1.5-3+2-0.5+1-2-2-2.5=-5.5(千克).
(25×8-5.5)×2.6=505.7(元).
答:出售这8筐白菜可卖505.7元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.

(1)求证:AB是⊙O的切线;
(2)若∠A=60°,DF=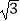 ,求⊙O的直径BC的长.
,求⊙O的直径BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个两位数恰等于它的各位数字之和的
 倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个.
倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx与直线y=2x+4交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作x轴、y轴的平行线与直线AB交于点C和点E.
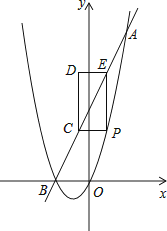
(1)求抛物线的解析式;
(2)若C为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习一次函数的经验,对函数y=|2x﹣1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=|2x﹣1|的自变量x的取值范围是 ;
(2)已知:
①当x=
 时,y=|2x﹣1|=0;
时,y=|2x﹣1|=0; ②当x>
 时,y=|2x﹣1|=2x﹣1
时,y=|2x﹣1|=2x﹣1③当x<
 时,y=|2x﹣1|=1﹣2x;
时,y=|2x﹣1|=1﹣2x;显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m= ;n= ;:
x
…
﹣2
0

1
m
…
y
…
5
1
0
1
n
…
(4)在平面直角坐标系xOy中,作出函数y=|2x﹣1|的图象;
(5)根据函数的图象,写出函数y=|2x﹣1|的一条性质.

-
科目: 来源: 题型:
查看答案和解析>>【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
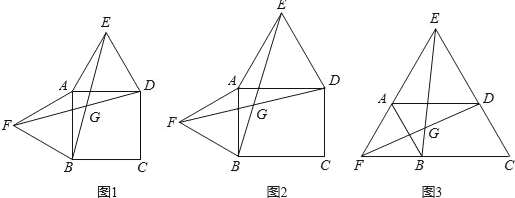
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
相关试题

