【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.

(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
参考答案:
【答案】(1)∠DOF=110° (2)∠COH=107.5°
【解析】本题考查对顶角的定义、性质垂直定义、角平分线的定义和根据图形写出角的和差关系式
解:(1)∵AB、CD、EF相交于点O,∴∠AOC=∠BOD
∵EF⊥AB ∴∠AOF=∠BOF=∠AOE=∠BOE=90°
∵OG为∠COF的平分线,∴∠COG=∠GOF
∵∠AOC∶∠COG=4∶7
∴∠AOC∶∠GOF=4∶7,∠AOC∶∠COF=4∶14 ,∠AOC∶∠AOF=4∶18
∴∠AOC=∠BOD=20°
∠DOF=∠BOD+∠BOF=20°90°=110°
(2)由(1)知:∠AOC=∠BOD ,∠COG=∠GOF,∠AOF=∠BOF=90°
∵OH为∠DOG的平分线.∴∠DOH=∠GOH
∵∠AOC∶∠DOH=8∶29,∴∠BOD∶∠BOH=8∶21;
设∠BOD=8k,∠COG=∠GOF=x,则∠GOH=29k,∠BOH=21k ,由∠AOF=∠BOF=90°得
8k+2x=29k+21k-x 解得x=14k ,
代入29k+21k-14k=90°解得k=2.5°
∠COH=∠COH+∠COH+∠COH=14k+29k=43k=43×2.5°=107.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】OC把∠AOB分成两部分且有下列两个等式成立:
①∠AOC=
 直角+
直角+ ∠BOC;②∠BOC=
∠BOC;②∠BOC= 平角-
平角- ∠AOC,问∶
∠AOC,问∶(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点,已知OE=
 ,EF=3,求菱形ABCD的周长和面积.
,EF=3,求菱形ABCD的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 = ___________;(2)
= ___________;(2) =___________;(3)
=___________;(3) =___________;(4)
=___________;(4) =________;(5)
=________;(5) __________;(6)
__________;(6) =___;(7)
=___;(7) _____;(8)
_____;(8) =__________.
=__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.

(1)求证:AB是⊙O的切线;
(2)若∠A=60°,DF=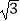 ,求⊙O的直径BC的长.
,求⊙O的直径BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个两位数恰等于它的各位数字之和的
 倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个.
倍,则这个两位数称为“巧数”.不是“巧数”的两位数有______个.
相关试题

