【题目】已知:在![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() .点
.点![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作
的右侧作![]() ,且
,且![]() ,
,![]() .
.
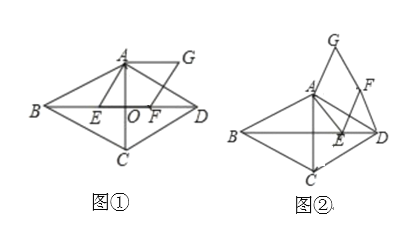
(1)如图①,若点![]() 落在线段
落在线段![]() 上,则线段
上,则线段![]() 与线段
与线段![]() 的数量关系是______;
的数量关系是______;
(2)如图②,若点![]() 不在线段
不在线段![]() 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
参考答案:
【答案】(1)AE=BE;(2)成立,理由见解析
【解析】
(1)先根据题意判断![]() 是菱形,再利用菱形的性质得出∠ABO=∠ADO=30°,AC⊥BD,即可求出∠FAD=30°即可得出结论;
是菱形,再利用菱形的性质得出∠ABO=∠ADO=30°,AC⊥BD,即可求出∠FAD=30°即可得出结论;
(2)先判断出△ACD和△AEF是等边三角形,进而得出∠CAE=∠DAF,即可判断出△ACE≌△ADF,即可得出结论.
(1)如图,连接AF,
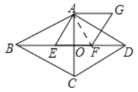
∵![]() ,且
,且![]() ,
,
∴四边形ABCD是菱形,
∴AC⊥BD,∠ABO=![]() ∠ABC=30°,
∠ABC=30°,
∴∠OAE=∠OAF=30°,
∴∠DAF=30°=∠ADO,
∴AF=FD,
∵AF=EF,
∴EF=FD;
∵∠AEF=60°,
∴∠BAE=30°=∠ABO,
∴AE=BE.
(2)成立,如图,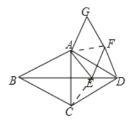
连接CE,AF,
∵四边形ABCD是菱形,四边形AEFG是菱形,
∴AD=CD,AE=EF,BD垂直平分AC,∠ABC=∠ADC=60°,
∴∠ADC=∠AEF=60°,
∴△ACD和△AEF是等边三角形,
∴AC=AD,AE=AF=EF,∠CAD=∠EAF=60°,
∴∠CAE=∠DAF,
在△ACE和△ADF中, 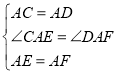 ,
,
△ACE≌△ADF(SAS),
∴EC=DF,
∵BD垂直平分AC,
∴EC=AE,
∴DF=AE=EF
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进了一批
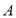 、
、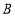 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:类型
进购数量(个)
进价(元/个)
售价(元/个)
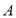 型
型20
1800
2300
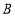 型
型40
1500
?
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则
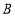 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,公交车行驶在笔直的公路上,这条路上有
 ,
,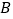 ,
,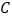 ,
,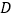 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从 站开往
站开往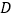 站的车称为上行车,从
站的车称为上行车,从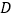 站开往
站开往 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从 站、
站、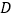 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 ,
,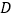 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
(1)问第一班上行车到
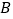 站、第一班下行车到
站、第一班下行车到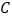 站分别用时多少?
站分别用时多少?(2)若第一班上行车行驶时间为
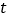 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为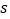 千米,求
千米,求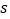 与
与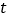 的函数关系式.
的函数关系式.(3)一乘客前往
 站办事,他在
站办事,他在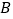 ,
,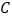 两站间的
两站间的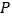 处(不含
处(不含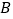 ,
,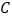 站),刚好遇到上行车,
站),刚好遇到上行车,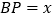 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到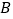 站或走到
站或走到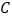 站乘下行车前往
站乘下行车前往 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求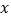 满足的条件.
满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.
 ∶
∶ C.
C. ∶
∶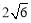 D.
D.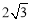 ∶
∶
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,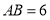 ,
, ,点
,点 是
是 边上一点,连接
边上一点,连接 ,把
,把 沿
沿 折叠,使点
折叠,使点 落在点
落在点 处.当
处.当 为直角三角形时,则
为直角三角形时,则 的长为________.
的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点
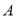 在直线
在直线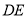 上,点
上,点 都在直线
都在直线 上(点
上(点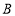 在点
在点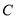 的左侧),连接
的左侧),连接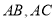 ,
,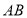 平分
平分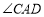 且
且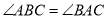

(1)如图1,求证:
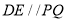
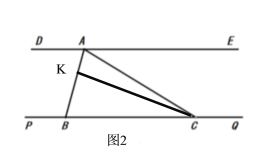
(2)如图2,点
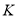 为
为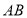 上一点,连接
上一点,连接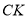 ,若
,若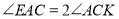 ,求
,求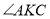 的度数
的度数(3)在(2)的条件下,点
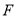 在直线
在直线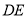 上,连接
上,连接 ,且
,且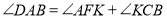 ,若
,若 ,求
,求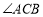 的度数(要求:在备用图中画出图形后,再计算)
的度数(要求:在备用图中画出图形后,再计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校检测学生跳绳水平,抽样调查了部分学生的“一分钟跳绳”成绩,并绘制了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
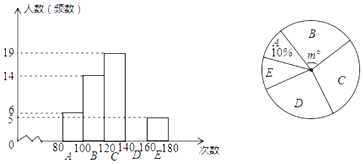
(1)抽样的人数是________人,补全频数分布直方图,扇形中
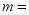 ________;
________;(2)本次调查数据的中位数落在________组;
(3)如果“一分钟跳绳”成绩大于等于120次为优秀,那么该校2250名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
相关试题

