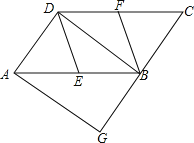
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处.当
处.当![]() 为直角三角形时,则
为直角三角形时,则![]() 的长为________.
的长为________.

参考答案:
【答案】![]() 或
或![]()
【解析】
当△CB′E为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示.
连结AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8-x,然后在Rt△CEB′中运用勾股定理可计算出x.再在Rt△ABE中,利用勾股定理可得AE的长
②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.可得AB=BE,在Rt△ABE中,利用勾股定理可得AE的长.
解:当△CEB′为直角三角形时,有两种情况:

①当点B′落在矩形内部时,如答图1所示.
连结AC,在Rt△ABC中,AB=6,BC=8,
∴AC=10,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=6,
∴CB′=10-6=4;
设BE=![]() ,则EB′=
,则EB′=![]() ,CE=
,CE=![]()
在Rt△CEB′中,由勾股定理可得:![]() ,
,
解得:![]()
在Rt△ABE中,利用勾股定理可得:![]()
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=6,
∴在Rt△ABE中,利用勾股定理可得:![]()
综上所述,![]() 的长为
的长为![]() 或
或![]()
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,公交车行驶在笔直的公路上,这条路上有
 ,
, ,
, ,
, 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从 站开往
站开往 站的车称为上行车,从
站的车称为上行车,从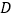 站开往
站开往 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从 站、
站、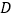 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在 ,
,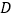 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
(1)问第一班上行车到
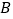 站、第一班下行车到
站、第一班下行车到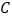 站分别用时多少?
站分别用时多少?(2)若第一班上行车行驶时间为
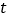 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为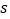 千米,求
千米,求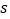 与
与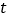 的函数关系式.
的函数关系式.(3)一乘客前往
 站办事,他在
站办事,他在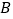 ,
,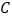 两站间的
两站间的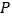 处(不含
处(不含 ,
, 站),刚好遇到上行车,
站),刚好遇到上行车,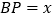 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到 站或走到
站或走到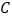 站乘下行车前往
站乘下行车前往 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求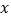 满足的条件.
满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.
 ∶
∶ C.
C. ∶
∶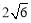 D.
D.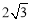 ∶
∶
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
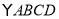 中,
中,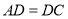 ,
,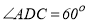 ,对角线
,对角线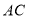 ,
,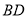 相交于点
相交于点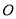 .点
.点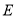 是线段
是线段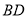 上一动点(不与
上一动点(不与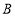 、
、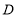 重合),连接
重合),连接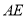 ,以
,以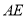 为边在
为边在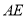 的右侧作
的右侧作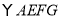 ,且
,且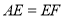 ,
,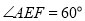 .
.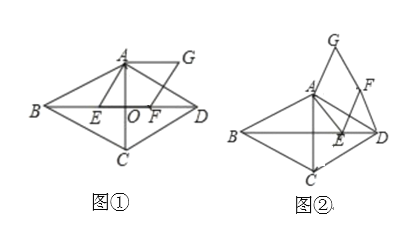
(1)如图①,若点
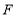 落在线段
落在线段 上,则线段
上,则线段 与线段
与线段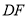 的数量关系是______;
的数量关系是______;(2)如图②,若点
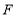 不在线段
不在线段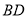 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点
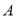 在直线
在直线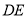 上,点
上,点 都在直线
都在直线 上(点
上(点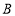 在点
在点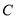 的左侧),连接
的左侧),连接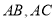 ,
,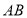 平分
平分 且
且

(1)如图1,求证:
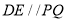
(2)如图2,点
 为
为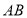 上一点,连接
上一点,连接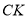 ,若
,若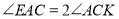 ,求
,求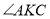 的度数
的度数(3)在(2)的条件下,点
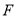 在直线
在直线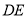 上,连接
上,连接 ,且
,且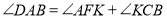 ,若
,若 ,求
,求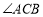 的度数(要求:在备用图中画出图形后,再计算)
的度数(要求:在备用图中画出图形后,再计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校检测学生跳绳水平,抽样调查了部分学生的“一分钟跳绳”成绩,并绘制了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
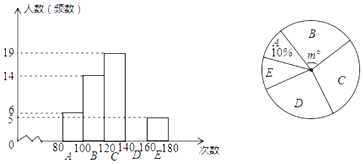
(1)抽样的人数是________人,补全频数分布直方图,扇形中
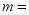 ________;
________;(2)本次调查数据的中位数落在________组;
(3)如果“一分钟跳绳”成绩大于等于120次为优秀,那么该校2250名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
相关试题

