【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于

A.3∶4 B.![]() ∶
∶![]() C.
C.![]() ∶
∶![]() D.
D.![]() ∶
∶![]()
参考答案:
【答案】D
【解析】
连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
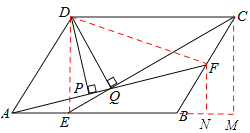
∵根据三角形的面积和平行四边形的面积得:
![]() ,即
,即![]() 。
。
∴AF×DP=CE×DQ,。
∵四边形ABCD是平行四边形,∴AD∥BC。
∵∠DAB=60°,∴∠CBN=∠DAB=60°。∴∠BFN=∠MCB=30°。
∵AB:BC=3:2,∴设AB=3a,BC=2a。
∵AE:EB=1:2,F是BC的中点,∴BF=a,BE=2a,BN=![]() a,BM=a。
a,BM=a。
由勾股定理得:FN=![]() a,CM=
a,CM=![]() a。
a。
∴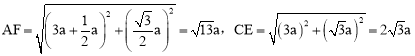 。
。
∴![]() 。∴
。∴![]() 。故选D。
。故选D。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小图暑假期间参加社会实践活动,从某批发市场以每个a元的价格购进50个手机充电宝,然后每个加价b元到市场出售.
(1)求全部售出50个手机充电宝的总销售额为多少元(结果用含a,b的式子表示)?
(2)由于开学临近,小丽在成功售出30个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含a、b的式子表示)
③若a=2b,小丽实际销售完这批充电宝的利润率为 (利润率=利润÷进价100%).
-
科目: 来源: 题型:
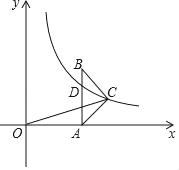
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=
 (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC= .
.(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2
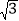 ,求DF的值;
,求DF的值;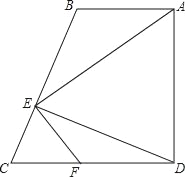
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形
 的顶点
的顶点 在坐标原点,顶点
在坐标原点,顶点 分别在
分别在 轴,
轴, 轴的正半轴上,
轴的正半轴上, ,
, 为边
为边 的中点,
的中点, 是边
是边 上的一个动点,当
上的一个动点,当 的周长最小时,点
的周长最小时,点 的坐标为_________.
的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则
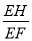 的值是( )
的值是( )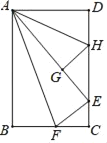
A.
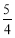 B.
B. 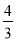 C.
C. 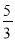 D.
D. 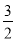
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法中不正确的是( )

A. ∠1与∠AOB是同一个角B. ∠AOC也可以用∠O表示
C. ∠β=∠BOCD. 图中有三个角
相关试题

