【题目】为了落实国务院惠农的指示精神,最近市政府又出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量![]() (千克)与销售价
(千克)与销售价![]() (元/千克)有如下关系:
(元/千克)有如下关系:![]() .设这种产品每天的销售利润为
.设这种产品每天的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
参考答案:
【答案】⑴![]() ⑵x=30时,y最大为200元⑶定为每千克25元
⑵x=30时,y最大为200元⑶定为每千克25元
【解析】
试题分析:(1)根据销售额=销售量×销售价单x,列出函数关系式;
(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值;
(3)把y=150代入(2)的函数关系式中,解一元二次方程求x,根据x的取值范围求x的值.
试题解析:(1)由题意得出:
w=(x-20)y
=(x-20)(-2x+80)
=-2x2+120x-1600,
故w与x的函数关系式为:w=-2x2+120x-1600;
(2)w=-2x2+120x-1600=-2(x-30)2+200,
∵-2<0,
∴当x=30时,w有最大值.w最大值为200.
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
(3)当w=150时,可得方程-2(x-30)2+200=150.
解得 x1=25,x2=35.
∵35>28,
∴x2=35不符合题意,应舍去.
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.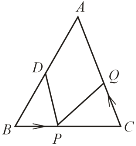
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若
 ,求出发几秒后,
,求出发几秒后, 为直角三角形?
为直角三角形?(3)若
 ,当
,当 的度数为多少时,
的度数为多少时, 为等腰三角形?(请直接写出答案,不必写出过程).
为等腰三角形?(请直接写出答案,不必写出过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】今年3月5日,实验中学组织全体学生参加了“走出校门,服务社会”的活动。九年级一班小明同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图。请根据小明同学所作的两个图形,解答:
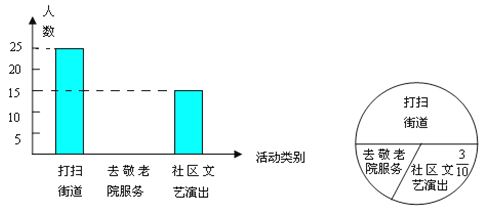
(1)九年级一班有多少名学生?
(2)补全直方图的空缺部分。
(3)若九年级有800名学生,估计该年级去敬老院的人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面有8个算式,排成4行2列
2+2, 2×2
3+
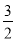 , 3×
, 3×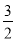
4+
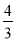 , 4×
, 4×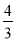
5+
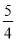 , 5×
, 5×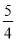
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+
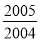 和2005×
和2005×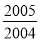 的结果相等吗?
的结果相等吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
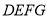 是
是 的内接矩形,如果
的内接矩形,如果 的高线
的高线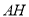 长
长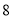
 ,底边
,底边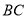 长
长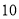
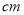 ,设
,设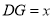
 ,
,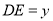
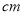 ,
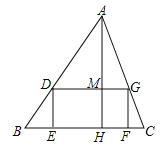
,
(1)求
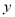 关于
关于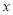 的函数关系式;
的函数关系式;(2)当
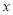 为何值时, 四边形
为何值时, 四边形 的面积最大?最大面积是多少?
的面积最大?最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】我校初一的学生要步行到20千米的郊外春游.(1)班学生组成前队,步行速度为4千米/时,(2)班学生组成后队,速度为6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)后队出发几小时后两队相距3千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米1.3元;超过5千米,每千米2.4元。
(1)若某人乘坐了
 (
(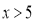 )千米的路程,则他应支付的费用是多少?
)千米的路程,则他应支付的费用是多少?(2)若某人乘坐的路程为6千米,那么他应支付的费用是多少?
相关试题

