【题目】如图1.在菱形ABCD中,AB=2 ![]() ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.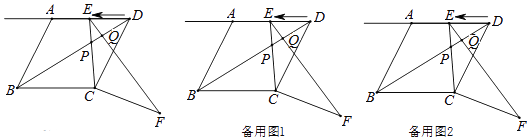
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形?
参考答案:
【答案】
(1)
证明:菱形ABCD中,BC=CD,
由旋转的性质可知,CE=CF,
∴ ![]() =
= ![]() ,
,
又∵∠FCE=∠DCB=α,
∴△FCE∽△DCB
(2)
由(1)知,△FCE∽△DCB,
∴当CE=CB=CD时,△FCE≌△DCB;
①E、D重合,此时t=0;
②如图,过点C作CM⊥AD,
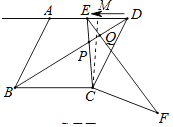
当EM=MD时,EC=CD,
Rt△CMD中,MD=CDcos∠CDA=2 ![]() ×
× ![]() =2,
=2,
∴t=ED=2MD=4,
∴当t=0或4时,△FCE≌△DCB
(3)
∵CE=CF,∴∠CEQ<90°.
①当∠EQD=90°时,
∠ECF=∠BCD,BC=DC,EC=FC,
∴∠CBD=∠CEF,
∵∠BPC=∠EPQ,
∴∠BCP=∠EQP=90°.
在Rt△CDE中,∠CED=90°,
∵AB=CD=2 ![]() ,tan∠ABC=tan∠ADC=2,
,tan∠ABC=tan∠ADC=2,
∴DE=2,
∴t=2秒;
②当∠EPQ=90°时,
∵菱形ABCD对角线AC⊥BD,
∴EC和AC重合.
∴DE=2 ![]() ,
,
∴t=2 ![]() 秒;
秒;
∴当t=2或者2 ![]() 时,△APQ为直角三角形.
时,△APQ为直角三角形.
【解析】(1)根据对应边成比例、夹角相等的两个三角形相似证明;(2)根据全等三角形的性质、余弦的概念计算;(3)分∠EQD=90°、∠EPQ=90°两种情况,根据正切的概念、菱形的性质解答.
【考点精析】解答此题的关键在于理解相似图形的相关知识,掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图形找出规律,并解答问题.
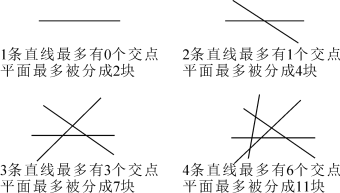
(1)5条直线相交,最多有_____个交点,平面最多被分成_____块;
(2)n条直线相交,最多有__________个交点,平面最多被分成____________块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)统计图共统计了天的空气质量情况;
(2)请将条形统计图补充完整;;空气质量为“优”所在扇形的圆心角度数是;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
 x与反比例函数y=
x与反比例函数y=  在第一象限内的图象相交于点A(m,3).
在第一象限内的图象相交于点A(m,3).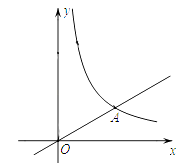
(1)求该反比例函数的关系式;
(2)将直线y=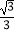 x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;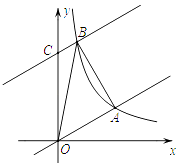
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.
x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.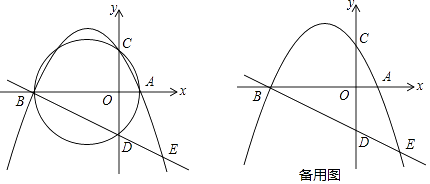
(1)求此抛物线的表达式及圆心M的坐标;
(2)设P为弧BC上任意一点(不与点B,C重合),连接AP交y轴于点N,请问:APAN是否为定值,若是,请求出这个值;若不是,请说明理由;
(3)延长线段BD交抛物线于点E,设点F是线段BE上的任意一点(不含端点),连接AF.动点Q从点A出发,沿线段AF以每秒1个单位的速度运动到点F,再沿线段FB以每秒 个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算:(a﹣b)2﹣a(a﹣2b);
(2)解方程: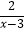 =
= 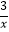 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某教育网站对下载资源规定如下:若注册VIP用户,则下载每份资源收
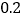 元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收
元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收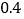 元,不收其它费用
元,不收其它费用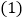 分别写出注册VIP用户的收费
分别写出注册VIP用户的收费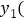 元
元 和注册普通用户
和注册普通用户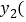 元
元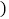 与下载数量
与下载数量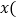 份
份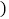 之间的函数关系式
之间的函数关系式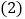 某学校每年要下载1500份资源,那么注册哪种用户比较合算?
某学校每年要下载1500份资源,那么注册哪种用户比较合算? 一年内下载多少份资源是两种用户收费一样?
一年内下载多少份资源是两种用户收费一样?
相关试题

