【题目】观察图形找出规律,并解答问题.
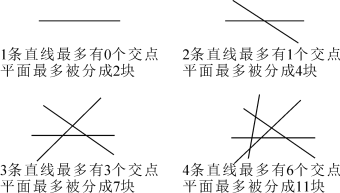
(1)5条直线相交,最多有_____个交点,平面最多被分成_____块;
(2)n条直线相交,最多有__________个交点,平面最多被分成____________块.
参考答案:
【答案】(1)10,16;(2)![]() ,[1+
,[1+![]() ]
]
【解析】
(1)根据每两条直线就有一个交点,可以列举出所有情况后再求解;
(2)根据列举的数值得出规律,再根据规律解题.
如图,

(1)任意画2条直线,它们最多有1个交点;
(2)任意画3条直线,它们最多有3个交点;
(3)任意画4条直线(只画交点个数最多的情况),最多有6个交点;
(4)5条直线最多有10个交点;
n条直线最多有![]() n(n-1)个交点.
n(n-1)个交点.
一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最多可以把平面分成7部分,四条直线最多可以把平面分成11部分,可以发现,两条直线时多了2部分,三条直线比原来多了3部分,四条直线时比原来多了4部分,…,n条时比原来多了n部分.
因为n=1,a1=1+1,
n=2,a2=a1+2,
n=3,a3=a2+3,
n=4,a4=a3+4,
…
n=n,an=an-1+n,
以上式子相加整理得,an=1+1+2+3+…+n=1+![]() .
.
当n=5时,1+![]() =16.
=16.
-
科目: 来源: 题型:
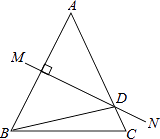
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.
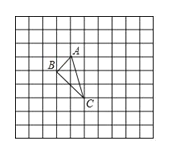
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)统计图共统计了天的空气质量情况;
(2)请将条形统计图补充完整;;空气质量为“优”所在扇形的圆心角度数是;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
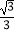 x与反比例函数y=
x与反比例函数y=  在第一象限内的图象相交于点A(m,3).
在第一象限内的图象相交于点A(m,3).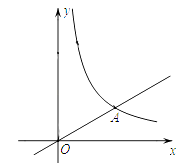
(1)求该反比例函数的关系式;
(2)将直线y=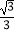 x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;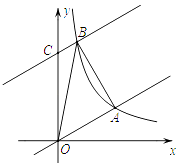
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1.在菱形ABCD中,AB=2
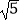 ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.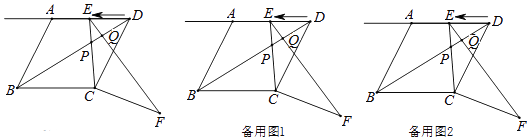
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形?
相关试题

