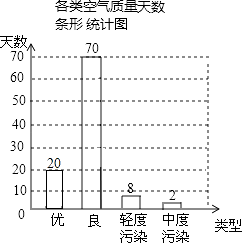
【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图. 
请根据图中信息,解答下列问题:
(1)统计图共统计了天的空气质量情况;
(2)请将条形统计图补充完整;;空气质量为“优”所在扇形的圆心角度数是;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是
参考答案:
【答案】
(1)100
(2) ;72°
;72°
(3)![]()
【解析】解:(1)∵良有70人,占70%, ∴统计图共统计了的空气质量情况的天数为:70÷70%=100(天);(2)如图:条形统计图中,空气质量为“优”的天数为100×20%=20(天),
空气质量为“优”所在扇形的圆心角度数是:20%×360°=72°,(3)画树状图得:
∵共有12种等可能情况,其中符合一男一女的有8种,
∴恰好选到一名男同学和一名女同学的概率是 ![]() =
= ![]() .
.
故答案为:(1)100,(2)72°,(3) ![]() .
.
(1)由良有70人,占70%,即可求得统计图共统计了几天的空气质量情况;(2)由条形统计图中,可得空气质量为“良”的天数为100×20%=20(天),空气质量为“优”所在扇形的圆心角度数是:20%×360°=72°,(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选到一名男同学和一名女同学的情况,再利用概率公式即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.
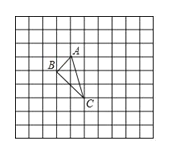
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图形找出规律,并解答问题.
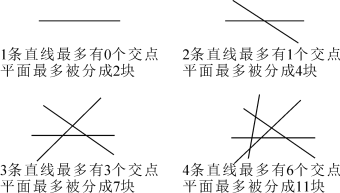
(1)5条直线相交,最多有_____个交点,平面最多被分成_____块;
(2)n条直线相交,最多有__________个交点,平面最多被分成____________块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
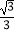 x与反比例函数y=
x与反比例函数y=  在第一象限内的图象相交于点A(m,3).
在第一象限内的图象相交于点A(m,3).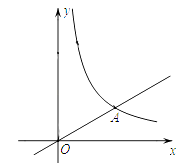
(1)求该反比例函数的关系式;
(2)将直线y=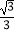 x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;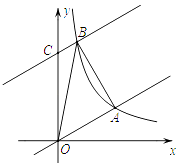
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1.在菱形ABCD中,AB=2
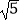 ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.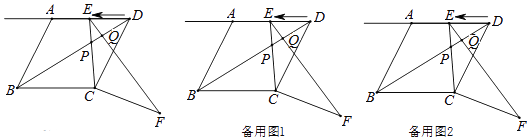
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.
x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.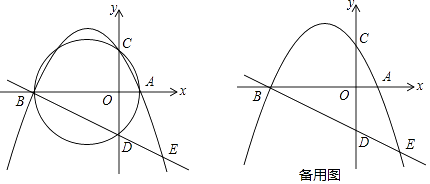
(1)求此抛物线的表达式及圆心M的坐标;
(2)设P为弧BC上任意一点(不与点B,C重合),连接AP交y轴于点N,请问:APAN是否为定值,若是,请求出这个值;若不是,请说明理由;
(3)延长线段BD交抛物线于点E,设点F是线段BE上的任意一点(不含端点),连接AF.动点Q从点A出发,沿线段AF以每秒1个单位的速度运动到点F,再沿线段FB以每秒 个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
相关试题

