【题目】计算下列各题
(1)计算:(a﹣b)2﹣a(a﹣2b);
(2)解方程: ![]() =
= ![]() .
.
参考答案:
【答案】
(1)解:原式=a2﹣2ab+b2﹣a2+2ab=b2
(2)解:两边乘x(x﹣3)得到2x=3(x﹣3)
解得x=9
经检验,x=9为原方程的根,
所以原方程的解为x=9
【解析】(1)利用完全平方公式展开,去括号合并同类项即可解决问题;(2)两边乘x(x﹣3),把分式方程转化为整式方程即可解决问题,注意必须检验;
【考点精析】本题主要考查了去分母法和单项式乘多项式的相关知识点,需要掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
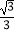 x与反比例函数y=
x与反比例函数y=  在第一象限内的图象相交于点A(m,3).
在第一象限内的图象相交于点A(m,3).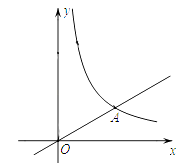
(1)求该反比例函数的关系式;
(2)将直线y=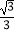 x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;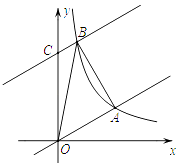
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1.在菱形ABCD中,AB=2
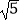 ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.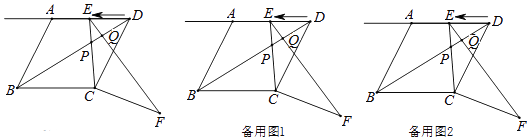
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.
x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.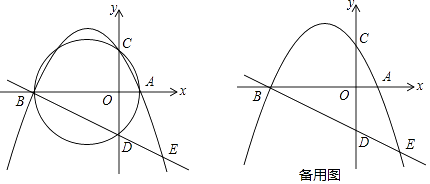
(1)求此抛物线的表达式及圆心M的坐标;
(2)设P为弧BC上任意一点(不与点B,C重合),连接AP交y轴于点N,请问:APAN是否为定值,若是,请求出这个值;若不是,请说明理由;
(3)延长线段BD交抛物线于点E,设点F是线段BE上的任意一点(不含端点),连接AF.动点Q从点A出发,沿线段AF以每秒1个单位的速度运动到点F,再沿线段FB以每秒 个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某教育网站对下载资源规定如下:若注册VIP用户,则下载每份资源收
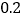 元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收
元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收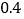 元,不收其它费用
元,不收其它费用 分别写出注册VIP用户的收费
分别写出注册VIP用户的收费 元
元 和注册普通用户
和注册普通用户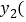 元
元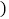 与下载数量
与下载数量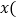 份
份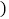 之间的函数关系式
之间的函数关系式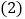 某学校每年要下载1500份资源,那么注册哪种用户比较合算?
某学校每年要下载1500份资源,那么注册哪种用户比较合算?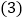 一年内下载多少份资源是两种用户收费一样?
一年内下载多少份资源是两种用户收费一样? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=
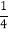 ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.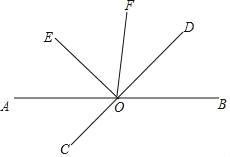
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:3+2=3×2-1,4+
 =4×
=4× -1,给出定义如下:
-1,给出定义如下:我们称使等式a+b=ab-1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,
 )都是“椒江有理数对”.
)都是“椒江有理数对”.(1)数对(-2,1),(5,
 )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(-n,-m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对” (注意:不能与题目中已有的“椒江有理数对”重复)
相关试题

