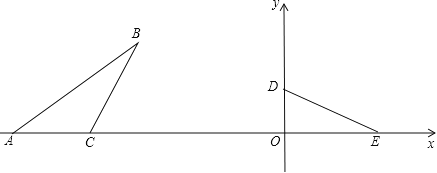
【题目】在平面直角坐标系xOy中,如图,已知Rt△DOE,∠DOE=90°,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5.∠ACB+∠ODE=180°,∠ABC=∠OED,BC=DE.按下列要求画图(保留作图痕迹):
(1)将△ODE绕O点按逆时针方向旋转90°得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN;
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与(1)中的△OMN的边NM重合;
(3)求OE的长.
参考答案:
【答案】(1)作图见解析;(2)作图见解析;(3)6.
【解析】
试题(1)以点O为圆心,以OE为半径画弧,与y轴正半轴相交于点M,以OD为半径画弧,与x轴负半轴相交于点N,连接MN即可.
(2)以M为圆心,以AC长为半径画弧与x轴负半轴相交于点A′,B′与N重合,C′与M重合,然后顺次连接即可.
(3)设OE=x,则ON=x,作MF⊥A′B′于点F,判断出B′C′平分∠A′B′O,再根据角平分线上的点到角的两边距离相等和角平分线的对称性可得B′F=B′O=OE=x,F C′="O" C′=OD=3,利用勾股定理列式求出A′F,然后表示出A′B′、A′O,在Rt△A′B′O中,利用勾股定理列出方程求解即可.
试题解析:解:(1)△OMN如图所示.
(2)△A′B′C′如图所示.
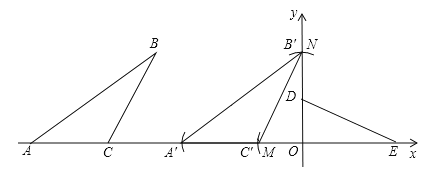
(3)设OE=x,则ON=x,如答图,过点M作MF⊥A′B′于点F,
由作图可知:B′C′平分∠A′B′O,且C′O⊥O B′,
∴B′F=B′O=OE=x,F C′="O" C′=OD=3,
∵A′C′=AC=5,∴![]() .∴A′B′=x+4,A′O=5+3=8.
.∴A′B′=x+4,A′O=5+3=8.
在Rt△A′B′O中,![]() ,解得x=6.
,解得x=6.
∴OE=6.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简
∣∣
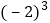
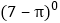
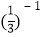
(2) 3
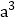 2
2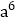 3
3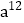
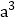
(3)
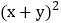 x yx 2y
x yx 2y (4) 3a b 23a b 2
(5)(3a+2)(3a-2)
(6)786- 786172 86
-
科目: 来源: 题型:
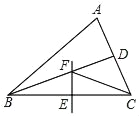
查看答案和解析>>【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=42°,则∠ABC=_____°.
-
科目: 来源: 题型:
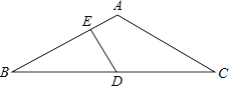
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AB于E,求EB:EA的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC、BD交于点O(如图),则图中全等三角形的对数为( )
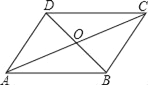
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
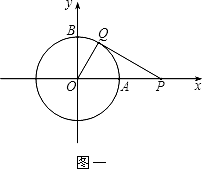
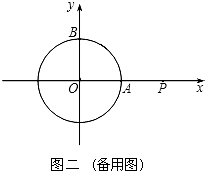
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
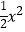 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).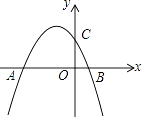
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
相关试题

