搜索
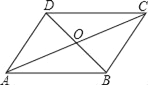
【题目】平行四边形ABCD中，对角线AC、BD交于点O（如图），则图中全等三角形的对数为（ ）
A. 2 B. 3 C. 4 D. 5
参考答案：
【答案】C
【解析】
平行四边形的性质是：对边相互平行且相等，对角线互相平分．这样不难得出：AD＝BC，AB＝CD，AO＝CO，DO＝BO，再利用“对顶角相等”就很容易找到全等的三角形：△ACD≌△CAB（SSS），△ABD≌△CDB（SSS），△AOD≌△COB（SAS），△AOB≌△COD（SAS）．
解：∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝BC；OD＝OB，OA＝OC；
∵OD＝OB，OA＝OC，∠AOD＝∠BOC；
∴△AOD≌△COB（SAS）；①
同理可得出△AOB≌△COD（SAS）；②
∵BC＝AD，CD＝AB，BD＝BD；
∴△ABD≌△CDB（SSS）；③
同理可得：△ACD≌△CAB（SSS）．④
因此本题共有4对全等三角形，故选C．
-
科目： 来源： 题型：
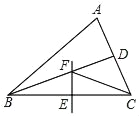
查看答案和解析>>【题目】如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A＝60°，∠ACF＝42°，则∠ABC＝_____°．
-
科目： 来源： 题型：
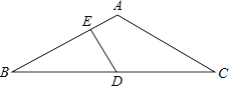
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，∠BAC=120°，D为BC的中点，DE⊥AB于E，求EB：EA的值．
-
科目： 来源： 题型：
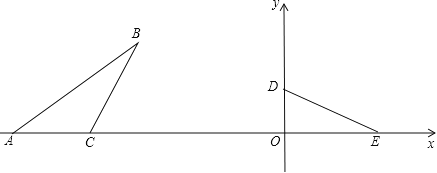
查看答案和解析>>【题目】在平面直角坐标系xOy中，如图，已知Rt△DOE，∠DOE=90°，OD=3，点D在y轴上，点E在x轴上，在△ABC中，点A，C在x轴上，AC=5．∠ACB+∠ODE=180°，∠ABC=∠OED，BC=DE．按下列要求画图（保留作图痕迹）：
（1）将△ODE绕O点按逆时针方向旋转90°得到△OMN（其中点D的对应点为点M，点E的对应点为点N），画出△OMN；
（2）将△ABC沿x轴向右平移得到△A′B′C′（其中点A，B，C的对应点分别为点A′，B′，C′），使得B′C′与（1）中的△OMN的边NM重合；
（3）求OE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】以坐标原点为圆心，1为半径的圆分别交x，y轴的正半轴于点A，B．
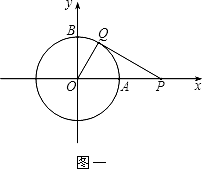
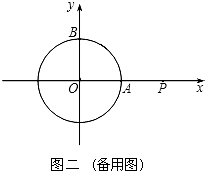
（1）如图一，动点P从点A处出发，沿x轴向右匀速运动，与此同时，动点Q从点B处出发，沿圆周按顺时针方向匀速运动．若点Q的运动速度比点P的运动速度慢，经过1秒后点P运动到点（2，0），此时PQ恰好是⊙O的切线，连接OQ．求∠QOP的大小；
（2）若点Q按照（1）中的方向和速度继续运动，点P停留在点（2，0）处不动，求点Q再经过5秒后直线PQ被⊙O截得的弦长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=﹣
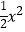+bx+c与y轴交于点C，与x轴的两个交点分别为A（﹣4，0），B（1，0）．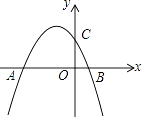
（1）求抛物线的解析式；
（2）已知点P在抛物线上，连接PC，PB，若△PBC是以BC为直角边的直角三角形，求点P的坐标；
（3）已知点E在x轴上，点F在抛物线上，是否存在以A，C，E，F为顶点的四边形是平行四边形？若存在，请直接写出点E的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
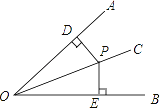
查看答案和解析>>【题目】证明命题“角的平分线上的点到角的两边的距离相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．
（1）已知：如图，∠AOC=∠BOC，点P在OC上，________
求证：________．
请你补全已知和求证
（2）并写出证明过程．
相关试题
