【题目】以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.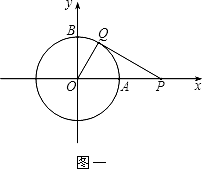
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长.
参考答案:
【答案】
(1)解:如图一,连接AQ.
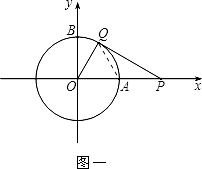
由题意可知:OQ=OA=1.
∵OP=2,
∴A为OP的中点.
∵PQ与⊙O相切于点Q,
∴△OQP为直角三角形.
∴ ![]() .
.
即△OAQ为等边三角形.
∴∠QOP=60°.
(2)解:由(1)可知点Q运动1秒时经过的弧长所对的圆心角为30°,若Q按照(1)中的方向和速度继续运动,那么再过5秒,则Q点落在⊙O与y轴负半轴的交点处(如图二).设直线PQ与⊙O的另外一个交点为D,
过O作OC⊥QD于点C,则C为QD的中点.
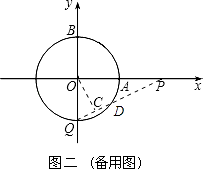
∵∠QOP=90°,OQ=1,OP=2,
∴QP= ![]() .
.
∵ ![]() ,
,
∴OC= ![]() =
= ![]() .
.
∵OC⊥QD,OQ=1,OC= ![]() ,
,
∴QC= ![]() =
= ![]() .
.
∴QD= ![]() .
.
【解析】(1)根据切线性质定理,以及OQ与OP之间的关系,可得出∠QOP的度数;(2)根据垂径定理及勾股定理解决本题即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AB于E,求EB:EA的值.
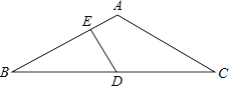
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,如图,已知Rt△DOE,∠DOE=90°,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5.∠ACB+∠ODE=180°,∠ABC=∠OED,BC=DE.按下列要求画图(保留作图痕迹):
(1)将△ODE绕O点按逆时针方向旋转90°得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN;
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与(1)中的△OMN的边NM重合;
(3)求OE的长.
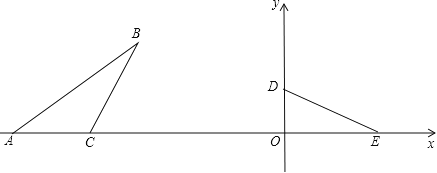
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC、BD交于点O(如图),则图中全等三角形的对数为( )
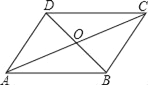
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
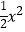 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).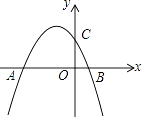
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
(1)已知:如图,∠AOC=∠BOC,点P在OC上,________
求证:________.
请你补全已知和求证
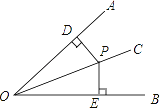
(2)并写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.

(1)求证:AB=CD;
(2)求证:CD2=BEBC;
(3)当CG=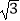 ,BE=
,BE=  时,求CD的长.
时,求CD的长.
相关试题

