【题目】如图,在平面直角坐标系xOy中,定义直线![]() 与双曲线
与双曲线![]() 的交点
的交点![]() 、n为正整数
、n为正整数![]() 为“双曲格点”,双曲线
为“双曲格点”,双曲线![]() 在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
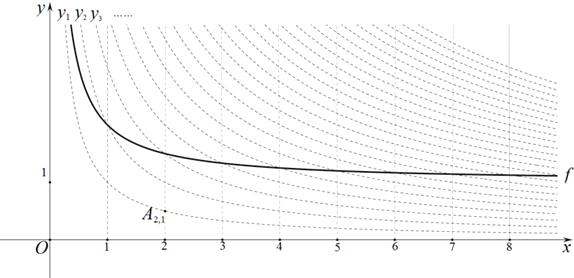
![]() “双曲格点”
“双曲格点”![]() 的坐标为______;
的坐标为______; ![]() 若线段
若线段![]() 的长为1个单位长度,则
的长为1个单位长度,则![]() ______;
______;
![]() 图中的曲线f是双曲线
图中的曲线f是双曲线![]() 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点![]() ,则f的解析式为
,则f的解析式为![]() ______;
______;
![]() 画出双曲线
画出双曲线![]() 的“派生曲线”
的“派生曲线”![]() 与双曲线
与双曲线![]() 不重合
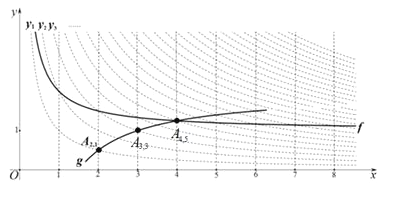
不重合![]() ,使其经过“双曲格点”
,使其经过“双曲格点”![]() 、
、![]() 、
、![]() .
.
参考答案:
【答案】(1) ![]() ,7;(2)
,7;(2) ![]() ;(3)见解析
;(3)见解析
【解析】试题分析:(1)①把![]() 代入
代入![]() ,即可求得点的纵坐标;
,即可求得点的纵坐标;
②首先求得![]() 的坐标,然后根据线段
的坐标,然后根据线段![]() 的长为1个单位长度即可求得n的值;
的长为1个单位长度即可求得n的值;
(2)把![]() 代
代![]() 求得点
求得点![]() 的坐标,然后设
的坐标,然后设![]() 的解析式为
的解析式为![]()
把点![]() 的坐标代入即可求得k的值,进而求得代数式;
的坐标代入即可求得k的值,进而求得代数式;
(3)首先求得“双曲格点”![]() 的坐标,把
的坐标,把![]() 进行上下平移或把
进行上下平移或把![]() 沿平行与x轴的直线翻折,进行平移即可求得.
沿平行与x轴的直线翻折,进行平移即可求得.
试题解析:(1)①把![]() 代入
代入![]() 得:
得: ![]()
则A的坐标是![]()
②把![]() 代入
代入![]() 得:
得: ![]()
根据题意得: ![]()
解得: ![]()
故答案为: ![]()
(2)把![]() 代
代![]() 得,
得, ![]() 则点
则点![]() 的坐标为:
的坐标为: ![]()
设![]() 的解析式为
的解析式为![]()
把![]() 代入,得
代入,得![]()
解得: ![]()
则![]() 的解析式为
的解析式为![]()
![]() 把
把![]() 代
代![]() 得,
得, ![]() 则点
则点![]() 的坐标为:
的坐标为: ![]()
把![]() 代
代![]() 得,
得, ![]() 则点
则点![]() 的坐标为:
的坐标为: ![]()
把![]() 代
代![]() 得,
得, ![]() 则点
则点![]() 的坐标为:
的坐标为: ![]()
如图所示:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知
 ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”
 ,必有实数根;
,必有实数根;(3)若 x 1是“勾系一元二次方程”
 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6 ,求ABC 的面积.
,求ABC 的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,
 的直角边AC在x轴上,
的直角边AC在x轴上,  ,反比例函数
,反比例函数 的图象经过BC边的中点
的图象经过BC边的中点 .
. 求这个反比例函数的表达式;
求这个反比例函数的表达式; 若
若 与
与 成中心对称,且
成中心对称,且 的边FG在y轴的正半轴上,点E在这个函数的图象上.
的边FG在y轴的正半轴上,点E在这个函数的图象上. 求OF的长;
求OF的长; 连接
连接 ,证明四边形ABEF是正方形.
,证明四边形ABEF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=4,对角线AC与BD交于点O,OE⊥AC交BC于点E,CE=3,则矩形ABCD的面积为( )

A.
 B.
B. C.12D.32
C.12D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个关于x的一元二次方程M:
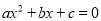 ;N:
;N: 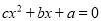 ,其中
,其中 ,有下列三个结论:
,有下列三个结论:①若方程M有两个相等的实数根,则方程N也有两个相等的实数根;
②若6是方程M的一个根,则
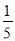 是方程N的一个根;
是方程N的一个根;③若方程M和方程N有一个相同的根,则这个根一定是
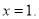 其中正确结论的个数是
其中正确结论的个数是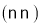
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场),一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军,为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜( )
A.10场B.11场C.12场D.13场
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
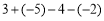 ;
; (2)
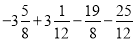
(3)﹣2.5÷
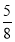 ×(﹣
×(﹣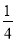 )
) (4)
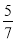 ÷(﹣2
÷(﹣2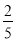 )﹣
)﹣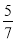 ×
×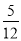 ﹣
﹣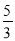 ÷4
÷4(5)
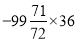
(6)(﹣2)2×5﹣(﹣2)3÷4
(7)
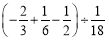 ;
; (8)
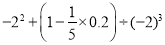 .
.
相关试题

