【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知![]() ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如![]() 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.

请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”![]() ,必有实数根;
,必有实数根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6![]() ,求ABC 的面积.
,求ABC 的面积.
参考答案:
【答案】(1)![]() (答案不唯一)(2)见解析(3)1.
(答案不唯一)(2)见解析(3)1.
【解析】
(1)直接找一组勾股数代入方程即可;
(2)根据根的判别式即可求解;
(3)根据方程的解代入求出a,b,c的关系,再根据完全平方公式的变形进行求解.
(1)当a=3,b=4,c=5时,
勾系一元二次方程为![]() ;
;
(2)依题意得△=(![]() )2-4ab=2c2-4ab,
)2-4ab=2c2-4ab,
∵a2+b2=c2,∴2c2-4ab=2(a2+b2)-4ab=2(a-b)2≥0,
即△≥0,故方程必有实数根;
(3)把x=-1代入得a+b=![]() c
c
∵四边形 ACDE 的周长是6![]() ,
,
即2(a+b)+ ![]() c=6
c=6![]() ,故得到c=2,
,故得到c=2,
∴a2+b2=4,a+b=2![]()
∵(a+b)2= a2+b2+2ab
∴ab=2,
故ABC 的面积为![]() ab=1.
ab=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,我们把横坐标、纵坐标都是整数的点称为整点
 如图,直线
如图,直线 和反比例函数
和反比例函数 的图象交于
的图象交于 两点,则落在图中阴影部分
两点,则落在图中阴影部分 不包含边界
不包含边界 内的整点个数有
内的整点个数有 个.
个.
A. 2
B. 3
C. 4
D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
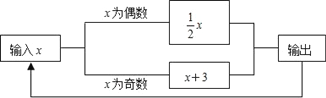
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,
 的直角边AC在x轴上,
的直角边AC在x轴上,  ,反比例函数
,反比例函数 的图象经过BC边的中点
的图象经过BC边的中点 .
. 求这个反比例函数的表达式;
求这个反比例函数的表达式; 若
若 与
与 成中心对称,且
成中心对称,且 的边FG在y轴的正半轴上,点E在这个函数的图象上.
的边FG在y轴的正半轴上,点E在这个函数的图象上. 求OF的长;
求OF的长; 连接
连接 ,证明四边形ABEF是正方形.
,证明四边形ABEF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=4,对角线AC与BD交于点O,OE⊥AC交BC于点E,CE=3,则矩形ABCD的面积为( )

A.
 B.
B. C.12D.32
C.12D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,定义直线
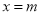 与双曲线
与双曲线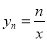 的交点
的交点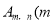 、n为正整数
、n为正整数 为“双曲格点”,双曲线
为“双曲格点”,双曲线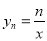 在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.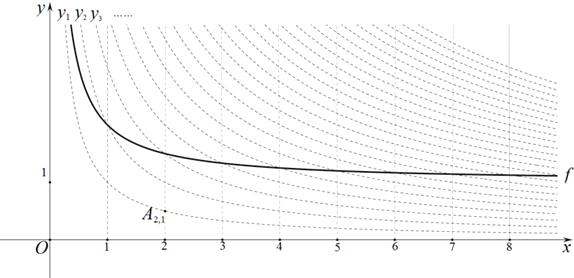
 “双曲格点”
“双曲格点”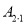 的坐标为______;
的坐标为______;  若线段
若线段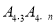 的长为1个单位长度,则
的长为1个单位长度,则 ______;
______;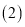 图中的曲线f是双曲线
图中的曲线f是双曲线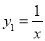 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点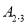 ,则f的解析式为
,则f的解析式为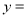 ______;
______;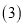 画出双曲线
画出双曲线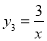 的“派生曲线”
的“派生曲线” 与双曲线
与双曲线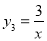 不重合
不重合 ,使其经过“双曲格点”
,使其经过“双曲格点”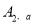 、
、 、
、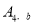 .
.
相关试题

