【题目】如图,在直角坐标系中, ![]() 的直角边AC在x轴上,
的直角边AC在x轴上, ![]() ,反比例函数
,反比例函数![]() 的图象经过BC边的中点
的图象经过BC边的中点![]() .
.
![]() 求这个反比例函数的表达式;
求这个反比例函数的表达式;
![]() 若
若![]() 与
与![]() 成中心对称,且
成中心对称,且![]() 的边FG在y轴的正半轴上,点E在这个函数的图象上.
的边FG在y轴的正半轴上,点E在这个函数的图象上.
![]() 求OF的长;
求OF的长;
![]() 连接
连接![]() ,证明四边形ABEF是正方形.
,证明四边形ABEF是正方形.

参考答案:
【答案】(1) ![]() ;(2)①1;②见解析
;(2)①1;②见解析
【解析】试题分析:(1)由D点坐标可求得k的值,可求得反比例函数的表达式;
(2)①由中心对称的性质可知![]() ≌
≌![]() ,由D点坐标可求得B点坐标,从而可求得BC和AC的长,由全等三角形的性质可求得GE和GF,则可求得E点坐标,从而可求得OF的长;②由条件可证得
,由D点坐标可求得B点坐标,从而可求得BC和AC的长,由全等三角形的性质可求得GE和GF,则可求得E点坐标,从而可求得OF的长;②由条件可证得![]() ≌
≌![]() 则可证得
则可证得![]() 且
且![]() 则可证得四边形
则可证得四边形![]() 为正方形.
为正方形.
试题解析:
![]() 反比例函数
反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
![]() ,
,
![]() 反比例函数表达式为
反比例函数表达式为![]() ;
;
![]() 为BC的中点,
为BC的中点,
![]() ,
,
![]() 与
与![]() 成中心对称,
成中心对称,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 点E在反比例函数的图象上,
点E在反比例函数的图象上,
![]() ,即
,即![]() ,
,
![]() ;
;
![]() 如图,连接AF、BE,
如图,连接AF、BE,

![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() 四边形ABEF为平行四边形,
四边形ABEF为平行四边形,
![]() ,
,
![]() 四边形ABEF为菱形,
四边形ABEF为菱形,
![]() ,
,
![]() 四边形ABEF为正方形.
四边形ABEF为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.

-
科目: 来源: 题型:
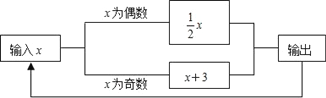
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知
 ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”
 ,必有实数根;
,必有实数根;(3)若 x 1是“勾系一元二次方程”
 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6 ,求ABC 的面积.
,求ABC 的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=4,对角线AC与BD交于点O,OE⊥AC交BC于点E,CE=3,则矩形ABCD的面积为( )

A.
 B.
B. C.12D.32
C.12D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,定义直线
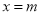 与双曲线
与双曲线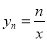 的交点
的交点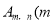 、n为正整数
、n为正整数 为“双曲格点”,双曲线
为“双曲格点”,双曲线 在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.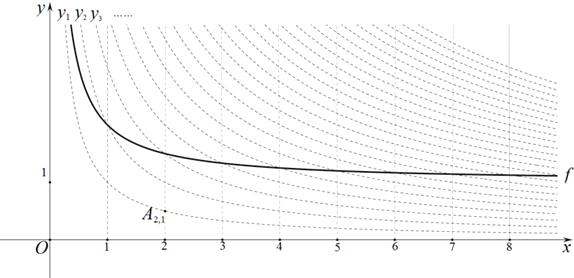
 “双曲格点”
“双曲格点”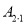 的坐标为______;
的坐标为______;  若线段
若线段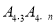 的长为1个单位长度,则
的长为1个单位长度,则 ______;
______;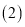 图中的曲线f是双曲线
图中的曲线f是双曲线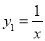 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点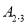 ,则f的解析式为
,则f的解析式为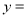 ______;
______; 画出双曲线
画出双曲线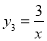 的“派生曲线”
的“派生曲线” 与双曲线
与双曲线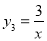 不重合
不重合 ,使其经过“双曲格点”
,使其经过“双曲格点”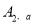 、
、 、
、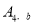 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个关于x的一元二次方程M:
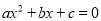 ;N:
;N: 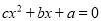 ,其中
,其中 ,有下列三个结论:
,有下列三个结论:①若方程M有两个相等的实数根,则方程N也有两个相等的实数根;
②若6是方程M的一个根,则
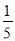 是方程N的一个根;
是方程N的一个根;③若方程M和方程N有一个相同的根,则这个根一定是
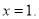 其中正确结论的个数是
其中正确结论的个数是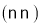
A. 0 B. 1 C. 2 D. 3
相关试题

