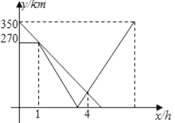
【题目】一辆货车从![]() 地匀速驶往相距350km的
地匀速驶往相距350km的![]() 地,当货车行驶1小时经过途中的
地,当货车行驶1小时经过途中的![]() 地时,一辆快递车恰好从
地时,一辆快递车恰好从![]() 地出发以另一速度匀速驶往
地出发以另一速度匀速驶往![]() 地,当快递车到达
地,当快递车到达![]() 地后立即掉头以原来的速度匀速驶往
地后立即掉头以原来的速度匀速驶往![]() 地.(货车到达
地.(货车到达![]() 地,快递车到达
地,快递车到达![]() 地后分别停止运动)行驶过程中两车与
地后分别停止运动)行驶过程中两车与![]() 地间的距离
地间的距离![]() (单位:
(单位:![]() )与货车从出发所用的时间
)与货车从出发所用的时间![]() (单位:
(单位:![]() )间的关系如图所示.则货车到达
)间的关系如图所示.则货车到达![]() 地后,快递车再行驶______
地后,快递车再行驶______![]() 到达
到达![]() 地.
地.
参考答案:
【答案】![]()
【解析】
由题意货车的速度=350-270=80km/h,设快递车的速度为![]() km/h,构建方程求出
km/h,构建方程求出![]() ,再求出相遇后两车分别到达目的地的时间即可解决问题.
,再求出相遇后两车分别到达目的地的时间即可解决问题.
由题意货车的速度=350-270=80km/h,设快递车的速度为![]() km/h,
km/h,
则有:![]() ,
,
解得:![]() =100,
=100,
∴两车相遇后,快递车需要![]() 小时到达C地,货车需要
小时到达C地,货车需要![]() 小时到达B地,
小时到达B地,
∴货车到达B地后,快递车再行驶![]() 到达C地.
到达C地.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:
我们知道,“两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化的作用.
已知三角板
 中,
中, ,长方形
,长方形 中,
中, .
.问题初探:
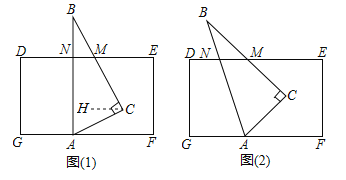
(1)如图(1),若将三角板
 的顶点
的顶点 放在长方形的边
放在长方形的边 上,
上,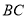 与
与 相交于点
相交于点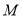 ,
,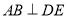 于点
于点 ,求
,求 的度数.
的度数.过点
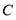 作
作 ,则有
,则有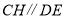 ,从而得
,从而得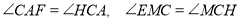 ,从而可以求得
,从而可以求得 的度数.
的度数.由分析得,请你直接写出:
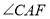 的度数为____________,
的度数为____________, 的度数为___________.
的度数为___________.类比再探:
(2)若将三角板
 按图(2)所示方式摆放(
按图(2)所示方式摆放(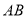 与
与 不垂直),请你猜想写出
不垂直),请你猜想写出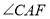 与
与 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是( )
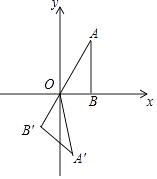
A.(2,﹣2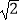 )
)
B.(2,﹣2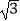 )
)
C.(2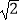 ,2)
,2)
D.(2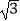 ,2)
,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,S△ABC=4
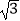 ,点P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为 .
,点P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为 . 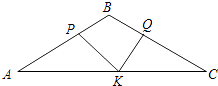
-
科目: 来源: 题型:
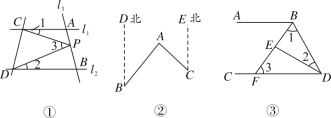
查看答案和解析>>【题目】(1)如图①,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是____;
(2)如图②,点A在B处北偏东40°方向,在C处北偏西45°方向,则∠BAC=____°.
(3)如图③,∠ABD和∠BDC的平分线交于点E,BE交AB于点F,∠1+∠2=90°,试说明:AB∥AB,并探究∠2与∠3的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )
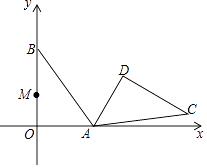
A.(0,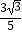 )
)
B.(0, )
)
C.(0,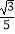 )
)
D.(0,3) -
科目: 来源: 题型:
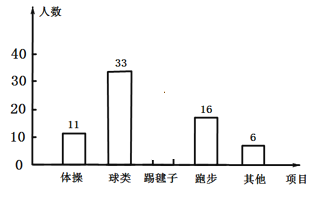
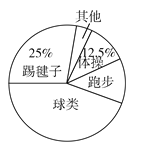
查看答案和解析>>【题目】为了了解全校3000名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的条形统计图和扇形统计图(均不完整).
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)补全条形统计图;
(3)求“球类”所对应的扇形的圆心角度数;
(4)估计该校3000名学生中有多少人最喜爱球类活动?
相关试题

