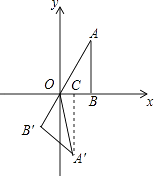
【题目】如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是( ) 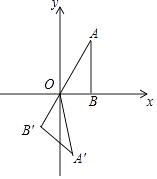
A.(2,﹣2 ![]() )
)
B.(2,﹣2 ![]() )
)
C.(2 ![]() ,2)
,2)
D.(2 ![]() ,2)
,2)
参考答案:
【答案】B
【解析】解:在直角△OAB中,∠AOB=90°﹣∠A=90°﹣30°=60°,
∠AOA'=120°,
则∠BOA'=∠AOA'﹣∠AOB=120°﹣60°=60°,
作A'C⊥OB于点C.
在直角△OA'C中,OA'=OA=4,
则A'C=OA'sin∠BOA'=4sin60°=4× ![]() =2
=2 ![]() ,OC=OA'cos∠BOA'=4cos60°=4×
,OC=OA'cos∠BOA'=4cos60°=4× ![]() =2,
=2,
则A'的坐标是(2,﹣2 ![]() ).
).
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线
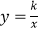 (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=  CB,AF=
CB,AF=  AB,且四边形OEBF的面积为2,则k的值为 .
AB,且四边形OEBF的面积为2,则k的值为 . 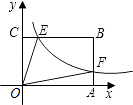
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2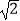 ,求线段EF的长.
,求线段EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:
我们知道,“两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化的作用.
已知三角板
 中,
中, ,长方形
,长方形 中,
中, .
.问题初探:
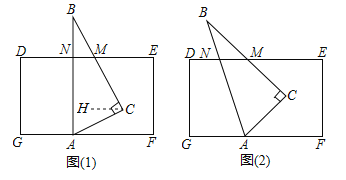
(1)如图(1),若将三角板
 的顶点
的顶点 放在长方形的边
放在长方形的边 上,
上, 与
与 相交于点
相交于点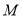 ,
,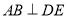 于点
于点 ,求
,求 的度数.
的度数.过点
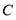 作
作 ,则有
,则有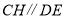 ,从而得
,从而得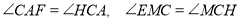 ,从而可以求得
,从而可以求得 的度数.
的度数.由分析得,请你直接写出:
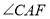 的度数为____________,
的度数为____________, 的度数为___________.
的度数为___________.类比再探:
(2)若将三角板
 按图(2)所示方式摆放(
按图(2)所示方式摆放(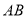 与
与 不垂直),请你猜想写出
不垂直),请你猜想写出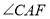 与
与 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,S△ABC=4
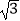 ,点P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为 .
,点P、Q、K分别为线段AB、BC、AC上任意一点,则PK+QK的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从
 地匀速驶往相距350km的
地匀速驶往相距350km的 地,当货车行驶1小时经过途中的
地,当货车行驶1小时经过途中的 地时,一辆快递车恰好从
地时,一辆快递车恰好从 地出发以另一速度匀速驶往
地出发以另一速度匀速驶往 地,当快递车到达
地,当快递车到达 地后立即掉头以原来的速度匀速驶往
地后立即掉头以原来的速度匀速驶往 地.(货车到达
地.(货车到达 地,快递车到达
地,快递车到达 地后分别停止运动)行驶过程中两车与
地后分别停止运动)行驶过程中两车与 地间的距离
地间的距离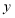 (单位:
(单位: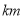 )与货车从出发所用的时间
)与货车从出发所用的时间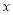 (单位:
(单位: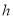 )间的关系如图所示.则货车到达
)间的关系如图所示.则货车到达 地后,快递车再行驶______
地后,快递车再行驶______ 到达
到达 地.
地.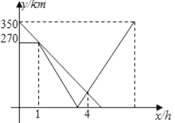
-
科目: 来源: 题型:
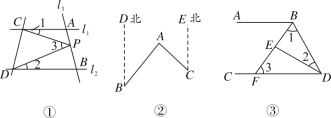
查看答案和解析>>【题目】(1)如图①,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是____;
(2)如图②,点A在B处北偏东40°方向,在C处北偏西45°方向,则∠BAC=____°.
(3)如图③,∠ABD和∠BDC的平分线交于点E,BE交AB于点F,∠1+∠2=90°,试说明:AB∥AB,并探究∠2与∠3的数量关系.
相关试题

