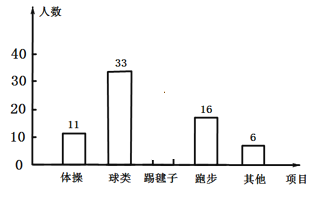
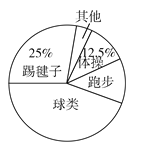
【题目】为了了解全校3000名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的条形统计图和扇形统计图(均不完整).
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)补全条形统计图;
(3)求“球类”所对应的扇形的圆心角度数;
(4)估计该校3000名学生中有多少人最喜爱球类活动?
参考答案:
【答案】(1) 88人;(2) 见解析;(3) ![]() ;(4) 1125人
;(4) 1125人
【解析】
(1)利用体操的频数和百分比即可求得答案;
(2)利用总数和踢毽子的百分比可求出其频数,补全图象即可;
(3)根据“球类”的人数即可得出扇形圆心角的度数;
(4)根据样本估计总体,即可得出估计全校最喜欢球类活动的人数.
(1)根据条形统计图知参加体操的人数为11人,占扇形图的12.5%,
∴11÷12.5%=88(人),
∴一共抽查了88人;
(2)踢毽子的人数=88×25%=22(人),
补全条形统计图如图所示:
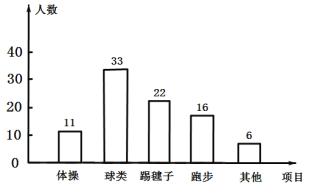
(3)扇形统计图中表示“球类”项目扇形圆心角的度数为![]() ;
;
(4)3000×![]() (人).
(人).
估计全校有1125人最喜欢球类活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从
 地匀速驶往相距350km的
地匀速驶往相距350km的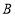 地,当货车行驶1小时经过途中的
地,当货车行驶1小时经过途中的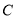 地时,一辆快递车恰好从
地时,一辆快递车恰好从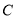 地出发以另一速度匀速驶往
地出发以另一速度匀速驶往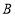 地,当快递车到达
地,当快递车到达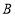 地后立即掉头以原来的速度匀速驶往
地后立即掉头以原来的速度匀速驶往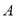 地.(货车到达
地.(货车到达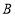 地,快递车到达
地,快递车到达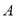 地后分别停止运动)行驶过程中两车与
地后分别停止运动)行驶过程中两车与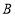 地间的距离
地间的距离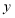 (单位:
(单位: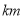 )与货车从出发所用的时间
)与货车从出发所用的时间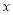 (单位:
(单位: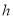 )间的关系如图所示.则货车到达
)间的关系如图所示.则货车到达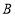 地后,快递车再行驶______
地后,快递车再行驶______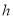 到达
到达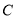 地.
地.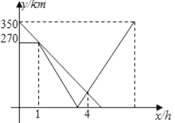
-
科目: 来源: 题型:
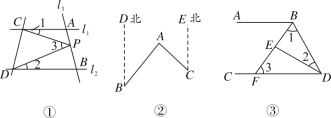
查看答案和解析>>【题目】(1)如图①,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是____;
(2)如图②,点A在B处北偏东40°方向,在C处北偏西45°方向,则∠BAC=____°.
(3)如图③,∠ABD和∠BDC的平分线交于点E,BE交AB于点F,∠1+∠2=90°,试说明:AB∥AB,并探究∠2与∠3的数量关系.
-
科目: 来源: 题型:
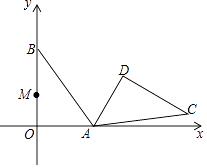
查看答案和解析>>【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )
A.(0,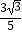 )
)
B.(0, )
)
C.(0,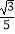 )
)
D.(0,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A在函数y1=﹣
 (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是边BC、AD上的点,有下列条件:
①AE∥CF;②BE=FD;③∠1=∠2;④AE=CF.
若要添加其中一个条件,使四边形AECF一定是平行四边形,则添加的条件可以是( )

A. ①②③④ B. ①②③ C. ②③④ D. ①③④
相关试题

