【题目】某校为了更好地开展“阳光体育一小时”活动,对本校学生进行了“写出你最喜欢的体育活动项目(只写一项)”的随机抽样调查,下面是根据得到的相关数据绘制的统计图的一部分.
抽样调查学生最喜欢的运动项目的人数统计图 各运动项目的喜欢人数占抽样总人数百分比统计图

请根据以上信息解答下列问题:
(1)该校对________名学生进行了抽样调查;
(2)请将图1和图2补充完整;
(3)图2中跳绳所在的扇形对应的圆心角的度数是________;
(4)若该校共有2400名同学,请利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?
参考答案:
【答案】(l)200;(2)见解析;(3)144o;(4)![]()
【解析】
(1)由最喜欢跳绳运动的人数及其所占百分比可得总人数;
(2)根据各组人数之和等于总人数求得最喜欢投篮运动的人数,再除以总人数可得其对应百分比,从而补全图1和图2;
(3)用360°乘以最喜欢跳绳运动的人数所占百分比可得跳绳所在的扇形圆心角的度数;
(4)总人数乘以样本中最喜欢跳绳运动的人数所占百分比即可得.
解:(1)被调查的学生总人数为80÷40%=200,
故答案为:200;
(2)最喜欢投篮运动的人数为200-(40+80+20)=60,
最喜欢投篮运动的人数所占百分比为![]() ×100%=30%,
×100%=30%,
补全图形如下: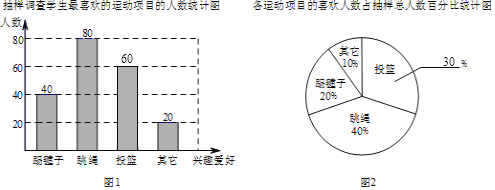
(3)图2中跳绳所在的扇形对应的圆心角的度数是为360°×40%=144°.
故答案为144°;
(4)2400×40%=960(人).
答:估计全校学生中最喜欢跳绳运动的人数约为960人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△ABC关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(1)求证:CF为⊙O的切线.
(2)若半径ON⊥AD于点M,CE=
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.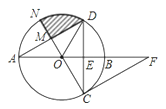
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
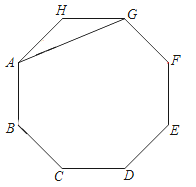
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AE⊥BC于点E,∠BAE=30°,AD=4cm.
(1)求菱形ABCD的各角的度数;
(2)求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长.
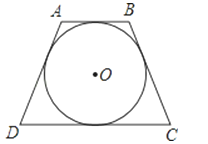
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图,在△
 中,把
中,把 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到 ,把
,把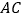 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 ,连接
,连接 ,当
,当 时,我们称△
时,我们称△ 是△
是△ 的“旋补三角形”,△
的“旋补三角形”,△ 边
边 上的中线
上的中线 叫做
叫做 的“旋补中线”,点
的“旋补中线”,点 叫做“旋补中心”.
叫做“旋补中心”.⑴ 特例感知:在如图、如图中,
 是
是 的“旋补三角形”,
的“旋补三角形”, 是
是 的“旋补中线”.
的“旋补中线”.① 如图,当
 为等边三角形时,
为等边三角形时, 与
与 的数量关系为
的数量关系为 =
=  ;
;② 如图,当
 ,
, 时,则
时,则 长为 .
长为 .⑵ 精确作图:如图,已知在四边形
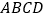 内部存在点
内部存在点 ,使得
,使得 是
是 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点 (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)⑶ 猜想论证:在如图中,当△
 为任意三角形时,猜想
为任意三角形时,猜想 与
与 的数量关系,并给予证明.
的数量关系,并给予证明.
相关试题

