【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
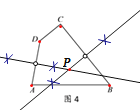
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

参考答案:
【答案】⑴ ① ![]() ② 4;⑵ 作图见解析;⑶
② 4;⑵ 作图见解析;⑶ ![]() ;见解析.
;见解析.
【解析】
(1)①首先证明△ADB′是含有30°是直角三角形,可得![]() ,即可解决问题;
,即可解决问题;
②首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
(2)作线段AD、BC的垂直平分线,交点即为点P.
(3)结论:![]() .如图1中,延长AD到M,使得AD=DM,连接E′M,C′M,首先证明四边形AC′MB′是平行四边形,再证明△BAC≌△AB′M,即可解决问题;
.如图1中,延长AD到M,使得AD=DM,连接E′M,C′M,首先证明四边形AC′MB′是平行四边形,再证明△BAC≌△AB′M,即可解决问题;
⑴ ①如图2,当△ABC为等边三角形时,AD与BC的数量关系为![]() ;
;
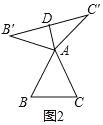
理由:∵△ABC是等边三角形,
∴AB=BC=AC=AB′=AC′,
∵DB′=DC′,
∴AD⊥B′C′,
∵![]()
∴![]()
∴![]()
∴![]()
故答案为:![]() .
.
②如图3,当![]() ,BC=8时,则AD长为4.
,BC=8时,则AD长为4.
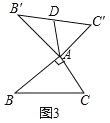
理由:∵![]()
∴![]()
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴![]()
故答案为:4.
⑵如图所示:(作线段AD、BC的垂直平分线,交点即为点P)
∴点P即为所求.
⑶ ![]()
证明:理由:如图1中,延长AD到M,使得AD=DM,连接E′M
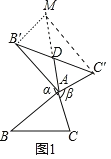
∵B′D=DC′,AD=DM,
∴四边形AC′MB′是平行四边形,
∴AC′=B′M=AC,
∵![]()
∴∠BAC=∠MB′A,
∵AB=AB′,
∴△BAC≌△AB′M,
∴BC=AM,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地开展“阳光体育一小时”活动,对本校学生进行了“写出你最喜欢的体育活动项目(只写一项)”的随机抽样调查,下面是根据得到的相关数据绘制的统计图的一部分.
抽样调查学生最喜欢的运动项目的人数统计图 各运动项目的喜欢人数占抽样总人数百分比统计图

请根据以上信息解答下列问题:
(1)该校对________名学生进行了抽样调查;
(2)请将图1和图2补充完整;
(3)图2中跳绳所在的扇形对应的圆心角的度数是________;
(4)若该校共有2400名同学,请利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AE⊥BC于点E,∠BAE=30°,AD=4cm.
(1)求菱形ABCD的各角的度数;
(2)求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长.
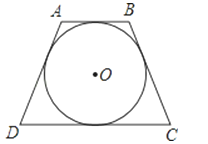
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA= 6
 cm,求AC的长.
cm,求AC的长.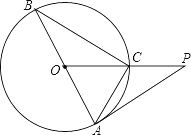
四、综合题(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点
 ,若点
,若点 的坐标为
的坐标为 (其中k为常数,且
(其中k为常数,且 ),则称点
),则称点 为点P的“k属派生点”.
为点P的“k属派生点”.例如:
 的“4属派生点”为
的“4属派生点”为 ,即
,即 .
.(1)点
 的“2属派生点”
的“2属派生点” 的坐标为________;
的坐标为________;(2)若点P的“3属派生点”
 的坐标为
的坐标为 ,求点P的坐标;
,求点P的坐标;(3)若点P在y轴的正半轴上,点P的“k属派生点”为
 点,且点
点,且点 到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师所在的学校为加强学生的体育锻炼,需要购买若干个足球和篮球,他曾两次在某商场购买过足球和篮球,两次购买足球和篮球的数量和费用如下表:
足球数量(个)
篮球数量(个)
总费用(元)
第一次
3
5
550
第二次
6
7
860
(1)求足球和篮球的标价;
(2)陈老师计划购买足球a个,篮球b个,可用资金最高为4000元;
①如果计划购买足球和篮球共60个,最多购买篮球多少个?
②如果可用资金恰好全部用完,且购买足球数量不超过篮球数量,则陈老师最多可购买足球________个.
相关试题

