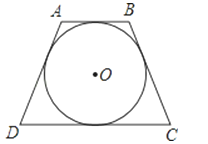
【题目】已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长.
参考答案:
【答案】60;18.
【解析】试题分析: (1)作AB⊥CD于E,BF⊥CD与F,因为⊙O为等腰梯形ABCD的内切圆,
根据切线长定理可得:AB+CD=AD+BC=20,因为AB∥CD,所以AE=6,所以等腰梯形ABCD的面积=![]() (AB+CD)AE=
(AB+CD)AE=![]() ×20×6=60,
×20×6=60,
(2)在Rt△ADE中,因为AD=10,AE=6,根据勾股定理可得DE![]() 8,因为梯形ABCD为等腰梯形,
8,因为梯形ABCD为等腰梯形,
所以CF=DE=8,根据(1)中AB+CD=20,AB=EF,所以8+8+2EF=20,解得EF=2,所以梯形的下底CD=8+2+8=18.
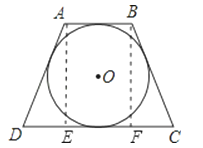
试题解析:作AB⊥CD于E,BF⊥CD与F,如图,
∵⊙O为等腰梯形ABCD的内切圆,
∴AB+CD=AD+BC=20,
∵AB∥CD,
∴AE=6,
∴等腰梯形ABCD的面积=![]() (AB+CD)AE=
(AB+CD)AE=![]() ×20×6=60,
×20×6=60,
在Rt△ADE中,
∵AD=10,AE=6,
∴DE=![]() 8,
8,
∵梯形ABCD为等腰梯形,
∴CF=DE=8,
而AB+CD=20,AB=EF,
∴8+8+2EF=20,解得EF=2,
∴梯形的下底CD=8+2+8=18.
-
科目: 来源: 题型:
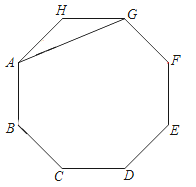
查看答案和解析>>【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地开展“阳光体育一小时”活动,对本校学生进行了“写出你最喜欢的体育活动项目(只写一项)”的随机抽样调查,下面是根据得到的相关数据绘制的统计图的一部分.
抽样调查学生最喜欢的运动项目的人数统计图 各运动项目的喜欢人数占抽样总人数百分比统计图

请根据以上信息解答下列问题:
(1)该校对________名学生进行了抽样调查;
(2)请将图1和图2补充完整;
(3)图2中跳绳所在的扇形对应的圆心角的度数是________;
(4)若该校共有2400名同学,请利用样本数据估计全校学生中最喜欢跳绳运动的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AE⊥BC于点E,∠BAE=30°,AD=4cm.
(1)求菱形ABCD的各角的度数;
(2)求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图,在△
 中,把
中,把 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得到
得到 ,把
,把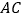 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 ,连接
,连接 ,当
,当 时,我们称△
时,我们称△ 是△
是△ 的“旋补三角形”,△
的“旋补三角形”,△ 边
边 上的中线
上的中线 叫做
叫做 的“旋补中线”,点
的“旋补中线”,点 叫做“旋补中心”.
叫做“旋补中心”.⑴ 特例感知:在如图、如图中,
 是
是 的“旋补三角形”,
的“旋补三角形”, 是
是 的“旋补中线”.
的“旋补中线”.① 如图,当
 为等边三角形时,
为等边三角形时, 与
与 的数量关系为
的数量关系为 =
=  ;
;② 如图,当
 ,
, 时,则
时,则 长为 .
长为 .⑵ 精确作图:如图,已知在四边形
 内部存在点
内部存在点 ,使得
,使得 是
是 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点 (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)⑶ 猜想论证:在如图中,当△
 为任意三角形时,猜想
为任意三角形时,猜想 与
与 的数量关系,并给予证明.
的数量关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA= 6
 cm,求AC的长.
cm,求AC的长.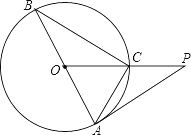
四、综合题(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点
 ,若点
,若点 的坐标为
的坐标为 (其中k为常数,且
(其中k为常数,且 ),则称点
),则称点 为点P的“k属派生点”.
为点P的“k属派生点”.例如:
 的“4属派生点”为
的“4属派生点”为 ,即
,即 .
.(1)点
 的“2属派生点”
的“2属派生点” 的坐标为________;
的坐标为________;(2)若点P的“3属派生点”
 的坐标为
的坐标为 ,求点P的坐标;
,求点P的坐标;(3)若点P在y轴的正半轴上,点P的“k属派生点”为
 点,且点
点,且点 到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
相关试题

